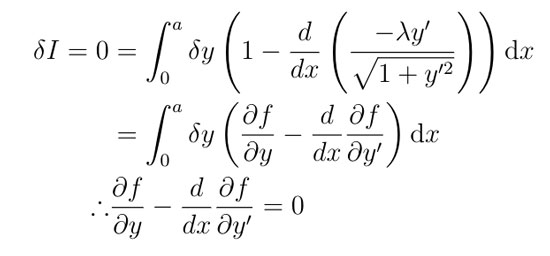En el artículo de hoy hablaremos sobre uno de los elementos matemáticos más populares, y usados en la práctica, las derivadas. Explicaremos qué son y mencionaremos ejemplos para facilitar su comprensión. A simple vista pueden parecer complicadas de entender, pero si prestas atención a los detalles y singularidades, es posible convertirse en un experto de las derivadas. Acompáñanos.
Tabla de contenidos
¿Qué son las derivadas?
Las derivadas son un cálculo diferencial, que es una rama de la matemática que estudia los cambios de las funciones, y una parte importante de los análisis matemáticos para calcular el valor del límite de la función. Pero, ¿a qué corresponde? Se trata de la cercanía entre un punto y otro. Entonces, cuando hablamos de una derivada nos referimos al valor en la que se transforma dicha función con respecto a una variable en la pendiente de la recta.
¿Para qué se usan las derivadas?
Las derivadas, en las matemáticas, se usan para una cantidad de aplicaciones diferenciales. Por ejemplo, para el cálculo de las aceleraciones, que es la variación de la velocidad y el tiempo de un punto a otro. También para el cálculo de las velocidades, que es la cantidad vectorial usada para medir el desplazamiento posicional en función al tiempo. Y, otro uso común de las derivadas es para optimizar las funciones, en específico, para maximizar o minimizar una función.
Cálculo de las derivadas
Sabemos qué son las derivadas y para qué se usan, pero, ¿cómo se calculan realmente? Existen dos métodos – según su definición y según las funciones–, los cuales explicaremos a continuación. También puedes hacer una calculadora de derivadas.
Según su definición
Es el método de cálculo de las derivadas más complicado por la cantidad de procedimientos a realizar, y en ocasiones suele ser muy complejo de entender. Quienes logran calcular las derivadas con este método demuestran una gran destreza en la rama de las matemáticas y no se recomienda para cálculos rápidos.
El método es conocido como diferenciación, procedimiento de determinación diferencial de una función. Por ejemplo, supongamos que tenemos una función determinada con ‘x’, y una vez que obtenemos la derivada que corresponde a la función ‘x’ se sustituye de acuerdo al valor, pero particularizando en el proceso.
Según las funciones
Es el método más usado y recomendado para calcular las derivadas cuando corresponde a análisis matemático. Debido a que según su definición suele cometerse errores y esta es una versión más sencilla de hacerlo. Para ello necesitaremos una tabla de derivadas, de donde sacaremos la información o fórmulas necesarias para conseguir el valor de una derivada en un punto de la tangente. Las tablas de las derivadas suelen ser generales, por lo que es sumamente importante memorizarlas. También vienen acompañadas de unas reglas.
Tabla de las derivadas
Como mencionamos anteriormente, las tablas de las derivadas son fórmulas e información usada para poder calcular el valor del límite de un punto de las funciones. Es una herramienta gráfica esencial para desarrollar con velocidad cálculos diferenciales, sin tener que emplear el método de definición, que es bastante complicado y tedioso.
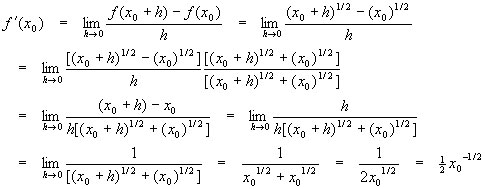
Sin embargo, la tabla debe ser memorizada, o mantenerla cerca cuando se vaya a calcular una derivada. Existen múltiples tipos de tablas para derivadas, como las derivadas compuestas. Aunque algunos la consideran innecesaria, ya que una vez que se domina la fórmula de la derivada tradicional, una compuesta no es un inconveniente.
Tipos de derivadas
Existen muchos tipos de derivadas que responden de acuerdo a la naturaleza del instrumento matemático para encontrar el valor del límite de una función en un determinado punto. Aquí mencionaremos los más relevantes y utilizados para simplificar la comprensión.
Derivadas de una función
Suelen ser las más comunes, y usadas en la práctica, de todas las alternativas diferenciales que existen. En primer lugar, expliquemos qué es una función. Es la relación entre un conjunto llamado dominio, y representado con ‘x’, con otra magnitud.
Entonces, cuando derivamos una función lo que estamos es buscando un punto determinado del límite del cociente. Por ejemplo, en f(x) buscamos un punto específico de x=a. Posteriormente en el gráfico se busca ese punto y se traza una línea de la derivada, sustituyendo el valor en la fórmula.
Derivadas algebraica
Las derivadas en algebraica corresponden a las pendientes de una tangente correspondiente a una función en un cierto punto. Aquí se encuentra la función en el determinado punto. Estas suelen ser cálculos matemáticos y ecuaciones de polinomios, donde cualquier valor es relativo.
Derivadas de un producto
En este caso las derivadas se obtienen mediante la multiplicación. Debemos multiplicar la derivada por el segundo producto que se encuentra en la ecuación matemática y luego se le suma por el segundo factor. Es un cálculo sencillo que responde a matemáticas de productos y operaciones binarias realizadas en ciertos contextos.
Derivadas del cociente
Las derivadas del cociente, que es la cantidad conseguida de la división de números, se obtienen mediante la multiplicación del denominador. También se debe multiplicar al mismo tiempo por el numerador.
Reglas de las derivadas
Las derivadas tienen ciertas reglas que deben seguirse al momento de realizar operaciones matemáticas. Conozcamos cuáles son y a qué responden en la práctica.
- Suma y resta de derivadas. La suma o resta de una derivada de dos funciones, corresponde a la suma y resta de las derivadas de las funciones.
- Derivadas del producto. Las derivadas de un producto, que es sinónimo de multiplicación, corresponde a la derivada de la primera función por la segunda.
- Derivada del cociente. Cuando existen dos funciones hay que multiplicar el denominador sin derivar y restar dicho numerador sin restar por la derivada del denominador. Luego, hay que dividirlo entre el denominador al cuadrado.
Ejemplos de una derivada
Ya sabemos la teoría y las nociones básicas para poder calcular las derivadas, ahora es momento de conocer algunos ejemplos sencillos para enriquecer el artículo. Presta atención.
En el caso número uno, si tenemos la siguiente función f(x) =-4x+2-, la derivada corresponde al punto f (x) =-4. En el caso número dos, si tenemos la siguiente función, f(x) = x5 –x3 +3, mediante la resolución, conseguimos que la derivada siguiente: f (x) = 5×4 –3×2.