El Teorema de Chebyshev es considerado una desigualdad probabilística, proporciona un límite superior a la probabilidad de que la desviación absoluta de una variable correspondiente o aleatoria, de su medida, excede un umbral dado. En general, el Teorema de Chebyshev se usa para medir la dispersión de los datos para cualquier distribución.
El Teorema de Chebyshev explica que al menos 1-1/k2 de datos de una muestra deben caer dentro de K, que es las desviaciones estándar de estándar de la media. En cualquier ejercicio o prueba, el K es un número real positivo mayor que uno.
En un conjunto de datos que se distribuye, o se encuentra en forma de curva de campana, este posee unas ciertas características interesantes que vale la pena resaltar. Uno de ellos se ocupa de la propagación de los datos, cuando se encuentra en relación con el número de la desviación estándar de la media.
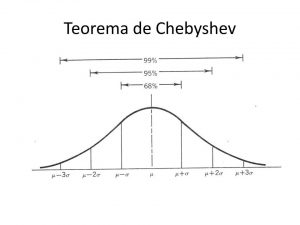
Cuando sucede una distribución normal, se sabe que al menos un 68% de los datos es una desviación estándar de la media. Por otro lado, el 95% son dos desviaciones están de la media, y el 99% aproximadamente se encuentra dentro de las tres desviaciones estándar de la media.
Sin embargo, si el conjunto de estos datos no se logra distribuir adecuadamente, en forma de curva de campana, entonces la cantidad diferente podría encontrarse dentro de una desviación estándar. El Teorema de Chebyshev es el encargado de explicar una manera de saber qué fracción de datos se encuentra dentro de las desviaciones estándar K de la media para cualquier conjunto de datos en específico.
A continuación, desglosaremos en detalle en qué consiste el Teorema de Chebyshev, así como ejemplos para que todos puedan entender de manera práctica cómo se puede aplicar. ¡Acompáñanos!
Tabla de contenidos
El Teorema de Chebyshev y los valores de confianza
Si ha tiene noción o un acercamiento con las estadísticas básicas o las probabilidades, entonces sabrá a qué se refiere la regla 68-95-99.7. Esta regla explica que, para una variable normalmente distribuida, aproximadamente el 68% de los valores caerán dentro de una desviación estándar de la media. Por otro lado, el 95% de los valores dentro de dos desviaciones estándar y el 99.7 dentro de tres desviaciones estándar.
Estos valores mencionados anteriormente, son bastante útiles para memorizar porque los valores que se calculan a partir de los datos a menudo se distribuyen aproximadamente normalmente debido al teorema del límite central. Tener una idea base de cómo los diferentes múltiplos de una desviación estándar corresponde a los intervalos de confianza, les permite a los usuarios comprender de manera más intuitiva la importancia de los gráficos, tablas y cálculos que incluyen valores de error de una desviación estándar.
Las distribuciones que son aproximadamente normales, son consideradas comunes, pero hay muchas circunstancias en que las que este no será el caso. La las distribuciones con una cola más pesada, se esperaría que haya menos de la distribución dentro de cada uno de los múltiplos de la desviación estándar. Mientras que para las distribuciones con una cola menos pesada, ocurriría completamente lo contrario. Para las distribuciones que no son normales, hay una gran probabilidad de que esos números 68/95/99.7 sean inexactos.
En caso que esté trabajando con una distribución de probabilidad que es desconocida, los valores de confianza para diferentes números de desviaciones estándar de la medida también resultarán desconocido. De encontrarse en esta situación, resultará útil tener una noción del ‘peor de los casos’ cuando los valores de confianza se encuentran bajo.
Características importantes del Teorema de Chebyshev
La desigualdad también se puede emplear con la frase de ‘datos de una muestra’ cuando se encuentra en una distribución de probabilidad. Lo anterior ocurre porque la desigualdad de Chebyshev es el resultado de la probabilidad, que luego se aplica en la estadística.
Se hace importante aclarar que esta desigualdad o Teorema de Chebyshev es un resultado que se ha aclarado y demostrado matemáticamente. Por lo que cada una de sus aplicaciones es completamente fidedignas, así como los resultados. No es como la relación empírica entre la media y el modo, o la regla general que conecta el rango y la desviación estándar.
¿Cuán tan dispersas son las mediciones del Teorema de Chebyshev?
Cuando se muestrea los datos del teorema, es útil saber cuán dispensables o dispersas son las mediciones en este rango. Por ejemplo, suponga que ha estado rastreando sus gastos de desayuno y, en promedio, gasta unos 10$ por día antes y durante el trabajo. Probablemente le interesaría saber si gastó constantemente esa cantidad o si tuvo unos gastos muy grandes que sesgaron el promedio general.
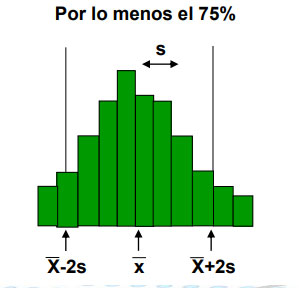
Por lo que vemos, es una excelente manera de ver estadísticamente cuántos gastos hemos hecho de acuerdo a la probabilidad estándar del Teorema de Chebyshev. Si bien esta ecuación a menudo da como resultado un rango relativamente amplio de valores, es útil porque solo requiere el conocimiento de la media y la desviación estándar, que se calculan fácilmente a partir de cualquier muestra o población de datos. El teorema también proporciona lo que podría llamarse una mirada en el peor de los casos de la dispersión de datos, como se mencionó anteriormente.
Formula del Teorema de Chebyshev
Para poder investigar este teorema, primero es necesario comparar los cálculos con la regla general 68-95-99.7 para distribuciones normales. Dado que esos números representan los datos que se encuentran dentro de los límites, se utiliza la desigualdad de Chebysgev para los datos dentro de los límites. Esta fórmula es la siguiente.
Probabilidad = 1 – (1 / k 2 )
Donde, matemáticamente, los valores menores o iguales a 1 no son válidos para este cálculo. Sin embargo, conectar los valores de k para 2 y 3 es más simple de lo que parece. En esos casos de 2 y 3, el Teorema de Chebyshev establece que al menos el 75% de los datos caerán dentro de las 2 desviaciones estándar de la media y se espera que el 89% de los datos caigan dentro de las 3 desviaciones estándar de la media.
Esto es menos preciso que los 95% y 99.7% que se pueden usar para una distribución normal conocida; sin embargo el Teorema de Chebyshev es cierta para todas las distribuciones de los datos, no solo para una distribución normal.
Ejemplo del Teorema de Chebyshev
Supongamos que se han muestreado los pesos de los perros en un determinado refugio de animales. Al analizar el muestreo, se ha descubierto que la muestra tiene una media de 20 libras con una desviación estándar de 3 libras. Con el uso del Teorema de Chebyshev. Sabiendo que el 75% de los perros que se han muestreado tienen pesos que son dos desviaciones estándar de la media. Dos veces la desviación estándar da un resultado de 2×3= 6. Restando y sumando esto, da una media de 20
Lo anterior solo nos dice que el 75% de los perros tienen un peso de 14 libras a 26 libras. Este es un ejemplo bastante práctico de cómo funciona el Teorema de Chebyshev o al menos cómo se puede emplear en un ejemplo de la vida real. La estadística se encuentra siempre al tanto.
Uso del Teorema de Chebyshev
Si sabemos más acerca de la distribución con la que se está trabajando, entonces se podrá garantizar que más datos estén a un cierto número de desviaciones estándar de la media. Por ejemplo, si se sabe la distribución normal, entonces el 95% de los datos son dos desviaciones estándar de la media. El Teorema de Chebyshev explica que en esta situación, sabremos que al menos el 75% de los datos son dos desviaciones estándar de la media. Tal como se mostró en el ejemplo anteriormente resuelto.
El valor de la desigualdad da un escenario de peor caso en el que lo único que sabemos sobre nuestros datos de muestra, o la distribución de probabilidad, es la media y la desviación estándar. Cuando no sabemos nada más sobre los datos, el Teorema de Chebyshev proporciona una idea adicional de cuán extendido es el conjunto de datos.
La ley de los grandes números
El Teorema de Chebyshev puede ser útil al hacer ciertas estimaciones aproximadas sobre los intervalos de confianza, pero a menudo también es una herramienta muy útil cuando se quieran probar casos estadísticos. Una muestra simple, pero bastante eficaz, donde el teorema se usa a menudo es en la ley de los grandes números. Por ejemplo, una gran prueba de esto sería:
La ley de los grandes números establece que para k, las variables aleatorias independientes e idénticamente distribuidas es la media muestral.

Límites del teorema
El Teorema de Chebyshev es importante por sus aplicaciones en el ámbito estadístico, y también su aplicabilidad a cualquier distribución. Como resultado de que sea general, es posible que, y generalmente no se debe hacer, proporcionar un límite tan agudo como los métodos alternativos que se pueden emplear si se conoce bien la distribución de la variable aleatoria. Para mejorar los límites de la nitidez de los resultados de la desigualdad, se ha desarrollado varios métodos como:
Variables estandarizadas
Los límites se pueden derivar primero estandarizando la variable aleatoria y obteniendo resultados más específicos.
Semivarianzas
Este es un método alternativo al estandarizado para obtener los límites más definidos mediante las variaciones parciales, también conocido como semivarianzas.
Distancia entre la media y la mediana
La variante unilateral puede usarse para probar la proposición de que para distribuciones de probabilidad que tienen un valor esperado y una media, la media y la mediana no pueden diferir entre sí en más de una desviación estándar.
