El Teorema de rolle es una teoría matemática que establece que si una función F es continua en el intervalo cerrado de a,b, y diferenciable en el intervalo abierto, tal que f (a) = f (b), entonces f ‘ (x) es igual a 0. Esto para algunos casos donde x sea menor a, b. En otras palabras, esto quiere decir, que si una curva continua pasa a través del mismo valor, que en este caso el eje es x, dos veces, y tiene una línea tangente única, considerada derivada, en cada punto del intervalo, entonces en algún momento entre los puntos finales tiene un paralelo tangente x.
Este teorema fue probado en el año 1691, por el matemático francés Michel Rolle, que es que lleva el nombre de dicho teorema. Sin embargo, no fue declarado valido con una prueba formal hasta el siglo XII. Esto cuando un matemático indio, conocido como Bhaskara II hizo la primera prueba resultando positivo.
Además der bastante útil para probar el teorema de valor medio, el Teorema de rolle no se suele usar con mucha frecuencia. La verdad es que estable solo la existencia de una solución y no su valor. Por los que los matemáticos prefieren emplear otras técnicas de solución para conocer el valor. Pero en cuanto se hace un análisis, de los casos especiales donde el teorema de valor medio está inmiscuido, es bastante normal que utilice el Teorema de rolle para hacer un cálculo diferencial.

A continuación, destacaremos cada uno de los detalles más importantes sobre este interesante teorema. Que, a pesar de no ser muy empleado, como quizás es el caso del Teorema de Norton en el campo de la electricidad, sigue formando parte de la formas de verificar una solución. ¡Acompáñanos hasta el final!
Tabla de contenidos
Enunciado del Teorema de Rolle
El enunciado del teorema de Rolle es muy popular en el mundo del algebra, aunque no tan utilizado en tiempos pasados, que dice el siguiente enunciado:
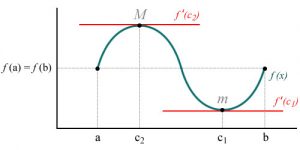
“Sea f una función continua en el intervalo cerrado [a,b], derivable en el intervalo abierto ]a,b[ y con f(a) = f(b). Entonces, existe al menos un punto c del intervalo] a,b[ que anula a la derivada de f.” – Michel Rolle
La interpretación es que, entre dos puntos en que una función continua, y una derivable, toman valores iguale, tiene que haber uno en el que la tangente es horizontal. En caso de que la función no sea constante, esto implicará que debe tener un extremo. Ahí es cuando se dice que las condicione del teorema de Rolle son suficientes, pero no realmente necesarias.
¿En qué consiste el Teorema de rolle?
La premisa básica, o la idea del Teorema de rolle es que si una función es continua, y se considera diferenciable en un intervalo, que tiene el mismo valor en los puntos finales; entonces la derivada será igual a cero en algún punto del intervalo que se está trabajo.
Cuando se ve gráficamente, esto significa que habrá una línea tangente horizontal en algún lugar del intervalo. Una función tiene dos puntos en el intervalo donde la derivada suele ser cero. Es función del Teorema de rolle garantizar la existencia donde estos se vuelven un solo punto.
Cuando se trata de cálculos, el lema de Rolle esencialmente establece que cualquier función diferenciable de valor real que alcance valores iguales en dos puntos distintos, debe tenerla menos un punto de estación en algún lugar de ellos. Esto también se puede plantear como que el teorema establece cómo encontrar el punto de la derivada, o más bien la pendiente de la línea tangente a la gráfica de la función, tiene un valor cero.
La razón principal por la que se aplica el Teorema de rolle es porque se necesita una prueba para el teorema de valor medio. De resto, muy pocos matemáticos lo utilizan en su campo.
Historia del Teorema de rolle
Fue el matemático francés Michel rolle que se encontraba vivo cuando Newton y Leibnitz inventaron el cálculo. Al principio, Rolle fue crítico con el cálculo una vez que los dos grandes científicos presentaron al mundo los modelos de cálculo. Sin embargo, una vez que entendió cómo funcionaba bien, cambió de opinión y demostró este teorema interesante que hemos venido desarrollo.
La primera vez que se probó el Teorema de rolle fue en el año 1691, solo siete años después de que se publicara el primer artículo sobre el cálculo. Así que se puede considerar una gran hazaña, ya que utilizó una forma de explicar soluciones complejas con tan pocos años de haberse publicado.
Sin embargo, es al matemático indio Bhaskara II quien se le atribuye el conocimiento popular del Teorema de rolle. La prueba que él realizo, así como los métodos de cálculo diferencial, que en ese momento de su vida consideró falaz. Se probó por primera vez por Cauchy en 1823, como corolario de una prueba del teorema de valor medio. Cosa que sigue realizando hasta el día de hoy.
Mientras que, el nombre, haciendo referencia a Michel Role, fue utilizado por primera vez en Alemania por Moritz Drobisch, en el año 1834. También se le adjudica, pero en Italia, y en el año 1846 a Giusto Bellavitis.

Historia de Michel Rolle
Michel Rolle, que nació en 1652 y murió en 1719, fue un gran matemático francés al que se le conoce por ser el autor de diversos resultados. Entre los que destaca, por supuesto, el teorema que lleva su nombre y enunciado se ha venido desarrollando a lo largo del artículo.
En sí, la infancia de rolle no fue agraciada con una formación académica, como si pudo haber sucedido con otros matemáticos con grandes teoremas. Sino que su formación fue autodidactica. Le encantaba los problemas así como encontrar las soluciones, siendo su principal acercamiento a las matemáticas.
Se dio a conocer ya en el año 1682, una vez que resolvió un problema propuesto por el matemático contemporáneo Jacques Ozanam. La solución de rolle, que con 32 años, ya se estaba dando a conocer. Por otro lado, unos años más tarde específicamente, empezaría a publicar obras relacionados con el mundo de la algebra. Siendo la más importante de todas el Traité d’algèbre. En la que hacía alusión de la notación para representar la raíz n-ésima de un número x.
Dicha solución sigue siendo aplicada hasta la actualidad. También, otra parte importante de esta obra, aunque no tiene ninguna demostración, es el método de las cascadas. Cosa que hoy sabemos que se ha probado y lleva el nombre de él mismo, Teorema de Rolle. Su función es obtener, o al menos aproximar las raíces de ecuaciones de cualquier grado.
Siguiendo con la demostración del teorema de rolle, en el área de los polinomios, y que no se basa en ningún tipo de cálculo diferencial, fue publicado posteriormente en una revista en el año 1691.
¿Por qué es necesario la función de rolle?
En el caso de la continuidad, se necesita el teorema porque las funciones que no son continuas en a,b, podría no tener un punto que tenga una línea tangente horizontal. En el caso de la diferenciabilidad, las funciones que son continuas, pero no diferenciables, tendrá una esquina o una cúspide en lugar del interval. Cuando esto sucede, es posible que no se tenga una línea tangente horizontal.
Ejemplo del Teorema de rolle
Para cuando un radio r> 0, su grafico es un semicírculo superior centrado en el origen. Esta función es continua en el intervalo cerrado, respectivamente. Mientras que, el diferencial, por otro lado, es el intervalo abierto que se señala con (-r,r). Pero, no es diferenciable en los puntos finales de ese mismo intervalo. Dado que f (- r) = f ( r ) se aplica el teorema de Rolle. De hecho, hay un punto donde la derivada de Fes cero tendrá en cuenta que el teorema se aplica cuando la función no se puede lograr diferenciar en los puntos finales. Ya que solo requiere que la función se diferenciable para que el intervalo se encuentre abierto.
Otros campos del Teorema de Rolle
El teorema de Rolle es una propiedad de funciones diferenciables quetrata los números reales en un campo ordenado. Por tanto, no se suele generalizar en otros campos, pero en un corolario sí. Este indica que si un factor polinomial real, que tiene todas sus raíces, sobre los números reales, entonces su derivada también lo hará.
Uno puede llamar a esta propiedad de un campo como propiedad de rolle. Los campos más generales no siempre tienen funciones diferenciables, pero siempre tienen polinomios, que se pueden diferenciar simbólicamente. Del mismo modo, los campos que son más generales, pueden no tener un orden en específico. Pero solo uno tendrá la noción de una raíz de un polinomio que se encuentra en un campo.
Así, el teorema de Rolle muestra que los números reales tiene la propiedad de Rolle. Cualquier otro campo cerrado algebraicamente como los números complejos, tiene la propiedad de rolle. Sin embargo, en el caso de los números racionales, no lo posee. Sino que la tendrán su derivada.
