El teorema de Bolzano es una hipótesis matemática intuitiva que se utiliza, entre otras cosas, para trazar gráficas de funciones continuas. También para hallar el valor aproximado de una ecuación donde existe la acotación de una raíz. Es de los modelos matemáticos más conocidos para obtener la solución a diversas ecuaciones.
Pero, ¿cómo funciona? ¿cuál es la historia detrás del análisis numérico? Estas, y más preguntas, serán respondidas en el siguiente artículo. Te invitamos a que nos acompañes hasta el final ya que esta información te servirá en el área estudiantil y profesional.
Tabla de contenidos
¿Qué es el teorema de Bolzano?
El teorema de Bolzano es una hipótesis matemática usada para funciones continuas definidas sobre en un intervalo con dos ejes. Fue presentada por el matemático Bernhard Bolzano en el año 1850 en República Checa.
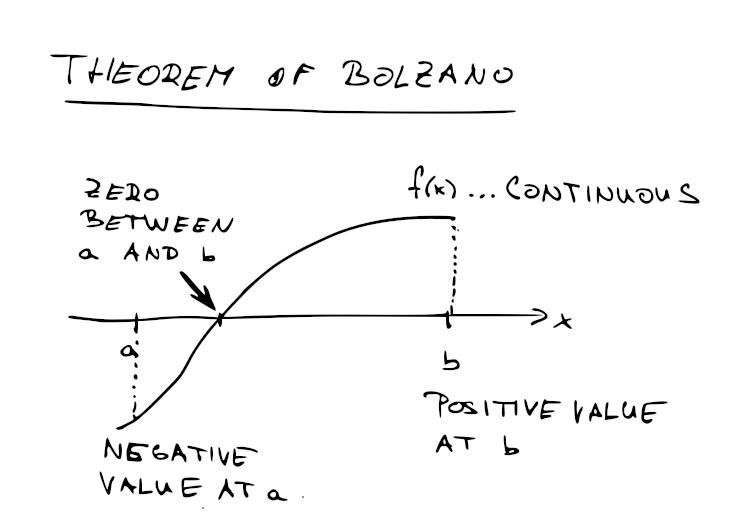
El supuesto se utiliza para probar la existencia de soluciones en ecuaciones dadas por funciones reales y continuas, dentro de un intervalo que toma valores positivos y negativos.
La tesis del teorema demuestra que, en algún punto del intervalo, la función se anula. Y uno de los requisitos para que se cumpla el teorema es que debe haber signos contrarios. Sin embargo, para entender mejor este supuesto hay que recordar cómo funciona la ley de los signos.
Historia del Teorema de Bolzano
Como bien te nombramos anteriormente, la creación de este teorema se le adjudica a Bernhard Bolzano, un matemático de República Checa originario de Praga. Estudió filosofía de la religión en la Universidad de la Praga y fue reconocido por ser un gran lógico con diversas aportaciones y obras solemnes. En especial sobre las funciones continuas, que es el tema de interés de este artículo.
La historia de este particular personaje es interesante, ya que en una instancia de su vida se le acusó de herejía y muchas de sus obras y aportaciones fueron censuradas por ir en contra de la política y la religión. Mientras se le vetó de usar su inteligencia en los diversos campos que manejaba, estudió en su gran obra y se hizo un nombre entre los matemáticos más reconocidos del país.
Al principio, sus obras no tuvieron la repercusión que sí encontró años después. Gran parte de la comunidad alegaba que no tenían el rigor necesario, ni mucho menos la profundidad para clasificar como un teorema matemático. Sin embargo, la historia demostró que algunos de los conceptos numéricos ‘redescubiertos’ fueron anticipados por Bolzano. Algunos ejemplos de los intelectuales que desarrollaron modelos, hipótesis y teoremas con trabajos del filósofo checo fueron: Cantor y Weierstrass.
Motivaciones previas al Teorema de Bolzano
Entre algunas de las motivaciones previas al teorema encontramos: ecuaciones que se podrían resolver fácilmente mediante un solo cálculo, simplificando el trabajo que otros realizaban. Tal es el caso de la conocida ‘X (2) -1 = 0.
También algunas ecuaciones que se podrían resolver mediante un cambio variable, como es el caso de la conocida “2(x+2) – 2( -x) + 3 = 0. La cual el matemático sustituyó cambiando la variable de la ecuación y consiguiendo un simple cálculo: y= 2(x). Siendo la solución a este problema: x = -2.

¿Qué dice el teorema de Bolzano?
El enunciado del teorema de Bolzano es el siguiente:
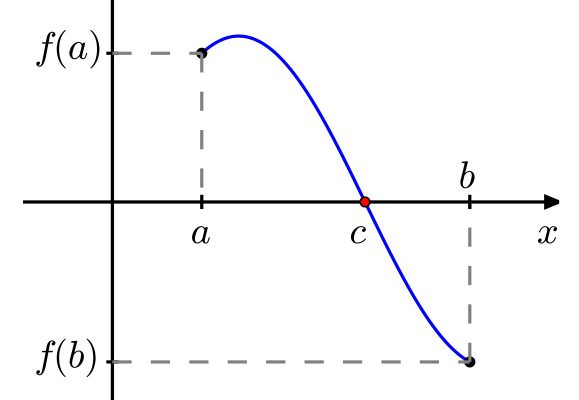
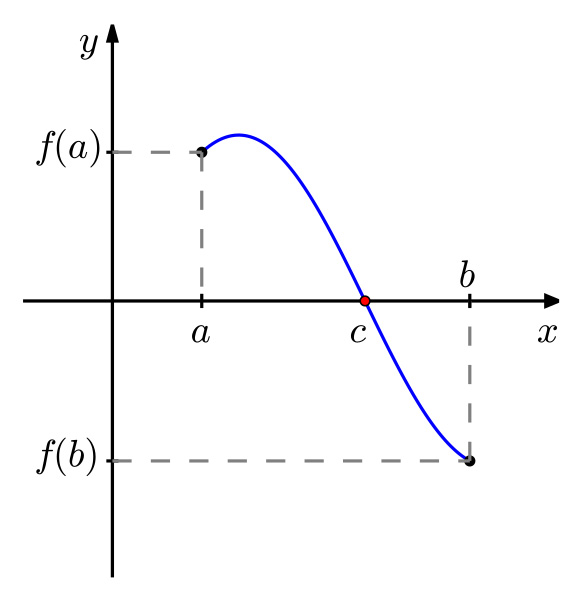
“Si una función f(x) está definida y es continua en un intervalo cerrado [a, b] y toma valores de distinto signo en los extremos a y b, entonces existe al menos un punto c del intervalo abierto (a, b) en el que se anula la función.”
Estudiando el enunciado nos damos cuenta que el autor explica que, en una función dada, la cual es continua y están conectados por una curva con dos extremos – f(a) y f(b) – en la que ‘f(a)’ se encuentra en el eje de las negativa de x, y en cambio ‘f(b)’ se encuentra en el eje de las positivas de x, existirá un punto de corte de la gráfica intermedio entre los valores ‘a’ y ‘b’, cuyo valor será igual a 0 y se representará mediante ‘f(c)’.
Aunado a las consideraciones anteriores, también podemos determinar mediante este enunciado que en toda función continua definida en un intervalo de f(a)*f(b) menor a 0, existirá una raíz dentro del intervalo. Lo que sucede con este teorema es que demuestra que ‘existe la raíz y también el corte de la gráfica’, pero no te indica dónde. Tampoco establece el número de los puntos existentes dentro del intervalo abierto, solo afirma que al menos existirá uno =1.
Demostración del Teorema de Bolzano
Para demostrar los conceptos establecidos en el Teorema de Bolzano, hemos decidido considerar la siguiente función: x³ + x − 1 = 0. Planteamos la función de la siguiente forma F(x)= x³ + x − 1 = 0, donde la función es continua por ser polinómica. (0,1). Bien, una vez trazada la gráfica nos damos cuenta que:
f(0) = -1 < en el eje inferior de las x, mientras que en el lado positivo de las x encontramos que f(1)= 1 >0. Cumpliendo con lo establecido en el teorema, ya que en los extremos del intervalos, los signos son diferentes. También que el punto c del intervalo abierto es el siguiente f(c) = 0.
Aplicación del Teorema de Bolzano
El teorema es una de las hipótesis más sencillas y fáciles de entender. La mayoría de las funciones se pueden resolver mediante un cálculo o con un cambio de las variables. Pero, existen otras situaciones, como el caso de las soluciones reales, donde no se pueden usar un simple cálculo y entonces hay que emplear el Teorema de Bolzano.
El teorema del checo también se aplica para probar, o al menos afirmar, la existencia de las soluciones de una ecuación dada en una función tanto real, como continua. Igualmente de una variable en un intervalo que tiene dos valores: uno positivo y otro negativo. Aunque esto último ya había sido proado por otros matemáticos mediante una construcción geométrica. Pero el teorema lo probó mediante una demostración analítica.
Aunado a las consideraciones anteriores, el teorema de Bolzano se utiliza en los siguientes casos: para encontrar un intervalo de al menos una solución, dividir el intervalo por la mitad y para evaluar la función en el punto medio. Esto último depende del signo del signo del valor.