La matemática es una ciencia que resulta bastante compleja y a menudo es aplicada en la vida cotidiana de las personas. Esta se caracteriza además de su complejidad por ser muy amplia. Una de las áreas que abarca esta es la relacionada con la teoría de los números, la cual se relaciona estrechamente con el teorema de Fermat.
Cuando hablamos de la teoría de los números, nos referimos a la rama de las matemáticas puras que se encarga del estudio de las propiedades de los números de forma general así como de los enteros en particular. Esto incluye además una variedad de problemas derivados del estudio de estos. Esta teoría fue reforzada por el jurista y matemático francés Pierre de Fermat, en el siglo XVII.
Recordemos que Fermat, fue un jurista aficionado a las matemáticas. Él solía retar a otros estudiosos como René Descartes y Blaise Pascal, con problemas y acertijos, matemáticos. De esta afición, nació lo que conocemos como el teorema de Fermat.
Además del teorema, Fermat hizo otros aportes a las matemáticas, como: el descubrimiento del cálculo diferencial o el principio fundamental de la geometría analítica. También junto con Pascal desarrolló la teoría de las probabilidades.
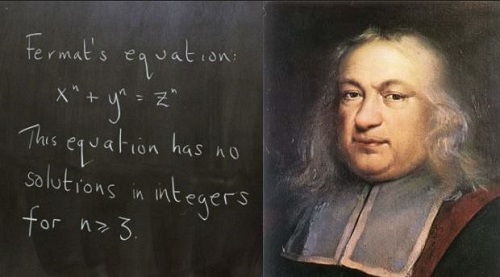
Tabla de contenidos
Historia del teorema de Fermat
El teorema de Fermat, como su nombre lo indica fue diseñado y desarrollado por el famoso jurista y matemático Pierre de Fermat. Él utilizaba el libro Arithmetica de Diofanto, para escribir comentarios y análisis al margen de cada problema. Esto les permitió a otros matemáticos como Leibniz y Newton entre otros, resolver dichos problemas.
Cabe destacar que, estos comentarios o análisis eran propuestas, que con frecuencia tenían solución. Sin embargo, en el problema VIII de este compendio, hizo Fermat el siguiente acertijo: tratar de encontrar un número cuadrado como suma de dos cuadrado. Esto también es conocido como ternas pitagóricas, y al cual no se le encontró solución. Fueron muchos los que intentaron darle solución, dentro de los que podemos mencionar al propio Fermat.
Pierre de Fermat fue el primero en avanzar en el desarrollo de este teorema. Lo hizo utilizando la conocida técnica del descenso infinito. Esta es una variante del principio de inducción, con la cual demostró el caso n=4. Posteriormente, el 3 de agosto de 1735 Leonhard Euler, se encargó de demostrar el caso n=3. Aunque esto resultó una falacia que se podía demostrar en el Álgebra de 1770, se consideró como una solución hecha por Euler.
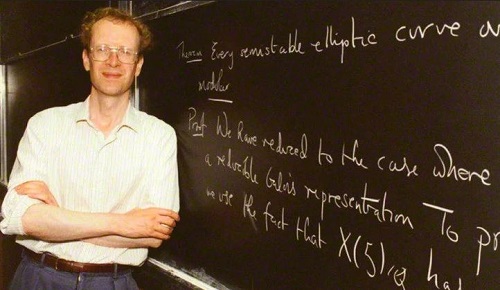
En el año 1993, fue que se hizo la demostración definitiva de dicho teorema. Esta fue hecha por el matemático inglés Andrew Wiles, quien luego de largos 8 años de investigación en solitario, hizo la demostración en público. Sin embargo, se encontró un error en esta, el cual fue corregido por el mismo Wiles junto con Richard Taylor. Dicha corrección tomó dos años y finalmente en 1995, el teorema de Fermat fue corroborado.
Teorema de Fermat
Como ya hemos visto, la demostración del teorema de Fermat llevó muchos años e incluso siglos. Y fueron muchos quienes lo intentaron, pero pocos pudieron hacer aportes para su demostración. Este postulado se convirtió en uno de los más grandes problemas en el área al que se enfrentaron durante 350 años los matemáticos.
Este complejo teorema, señala que: “Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado, en la suma de dos potencias de la misma clase. He descubierto para el hecho una demostración excelente. Pero este margen es demasiado pequeño para que (la demostración) quepa en él”.
Teorema de Fermat expresado en la notación actual
Este teorema enunciado, con la notación actual, se diría de la siguiente manera: Si se considera que n es un número entero con un valor mayor o igual que 3, entonces se dice que no existen números enteros positivos x, y y z, cumpliéndose de esta manera la igualdad: xn + yn= zn.
Aplicaciones del teorema de Fermat
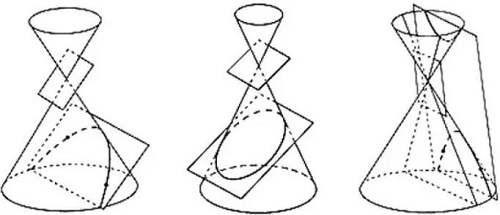
El teorema de Fermat con frecuencia es utilizado como un método para hallar tanto máximos como mínimos locales de lo que conocemos como funciones diferenciables en intervalos abiertos. Esto debido a que todos ellos son considerados como puntos estacionarios de la función. Es decir, son todos aquellos puntos donde la función derivada vale cero.
Aunque el postulado sólo señala la existencia de una condición para los máximos y mínimos de tipo local, este no está asociado con otra clase de puntos estacionarios. Tal es el caso de los puntos de inflexión, que no son considerados ni máximos ni mínimos.
Además, es importante tener en cuenta que, en los casos en los que exista la derivada segunda de la función, se puede determinar si el punto estacionario en cuestión es un máximo, un mínimo, o un punto de inflexión. Es necesario tener presente que el teorema de Fermat es un teorema de análisis real.
Existen otras aplicaciones para este teorema, dentro de las que podemos mencionar: aplicaciones teóricas, en las que se hace un análisis de la descomposición en producto de factores primos de determinados enteros. Criptografía asimétrica, la cual trabaja con un conjunto de claves, algunas de las cuales se establece haciendo uso de este teorema.
El test de primalidad, es otra de las aplicaciones de este principio. En este caso la base fundamental de este test la constituye el teorema de Fermat. Y por último, y no menos importante tenemos el número pseudoprimo, los cuales se caracterizan por pasar o aprobar el test de primalidad de Fermat algunas veces, lo cual permite reconocerlos como falsos primos.
Demostración del teorema de Fermat
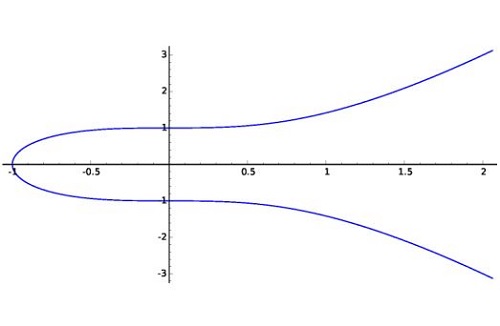
Andrew Wiles, demostró la veracidad de este teorema, y lo hizo basándose en la premisa que señala que, todas las curvas elípticas semiestables son racionales o son modulares. Estas curvas se desarrollan en espacios diferentes, sin embargo cuentan con un subconjunto de números que poseen una correspondencia en los dos sitios. Con esta premisa, Wiles transformó el teorema en un problema de curvas elípticas y formas modulares, el cual resultó de fácil resolución para todos.
