La geometría es una de las ramas de las matemáticas caracterizada por centrarse en el estudio de las propiedades de figuras que pueden ser en el plano o en el espacio. Dentro de esta rama se pueden encontrar los puntos, rectas, planos, politopos, entre otros. De esta parte se desprenden muchas cosas más, como suele suceder dentro de las matemáticas. Se tiene que tener en cuenta que es la base del dibujo técnico.
Dentro de todo el mundo de la geometría existen muchos teoremas, entre los cuales destaca el Teorema de los Ejes Paralelos o de Steiner. Se trata de uno de los teoremas de la geometría elemental, el cual en este caso fue creado por C. L. .Lehmus, pero que fue probado por Jakob Steiner.
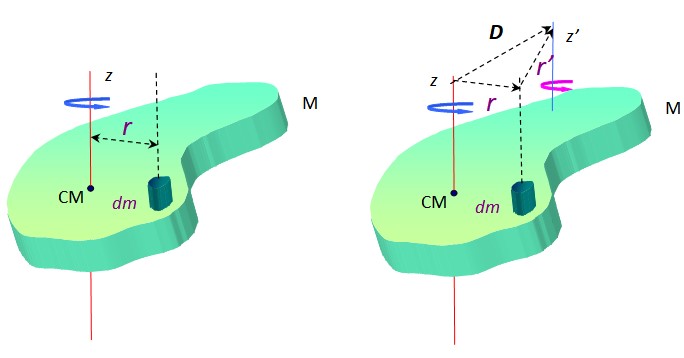
Se deberá de considerar el momento de inercia de un objeto plano: este va a tener su momento sobre un eje perpendicular al plano se considera la suma de los momentos de inercia cuando es sobre dos ejes. Esto quiere decir que ocurre un crece entre objetos en el plano que es perpendicular.
Esto es lo que se denomina como Teorema de ejes paralelos. No solamente es utilizada para los objetos planos. Sino que también es primordial para poder construir momentos de inercia sobre objetos tridimensionales. Uno de los casos puede ser el cilindro.
Historia del teorema de ejes paralelos
Debemos tener claro que el teorema de los ejes paralelos que también es conocido como el teorema de Steiner. Este teorema permite de forma sencilla poder evaluar el momento de inercia de un cuerpo plano. Esto en base a un eje que esta paralelo a otro que pase por el centro de la masa del objeto.
Este teorema debe su nombre a Jakob Steiner (1796 – 1863), el cual se encargó de afirmar que el ICM se defina como el momento de iniciar de un objeto, el cual es respecto a un eje que pasa por el centro CM e Iz es la forma en la cual se puede entender de forma muy sencilla este teorema. Que vamos a analizar un poco más a fondo.
Este matemático es de origen suizo, nació en la villa llamada Utzenstorf el lejano 18 de marzo de 1796. Fue un alumno destacado de Johann Heinrich Pestalozzi. Posteriormente, fue a realizar sus estudios hasta Heidelberg, para luego ir hasta Berlín donde pudo consagrarse como profesor y fue el fundador del diario denominado como Journal für die reine und angewandte Mathematik.
En el año de 1832 recibió un grado honorífico en la Universidad Königsberg, esto por el trabajo conocido como Systematische Entwickelungen. Fue uno de los que promovieron la introducción de una nueva cátedra que sería llamada geometría. Esto lo puedo hacer debido al apoyo de los hermanos Alexander y Wilhelm von Humboldt. Steiner. Murió el 1 de abril de 1863.
Ya con el paso de los años el teorema de los ejes paralelos tomo una gran importancia, mucho más en física. Esto debido a todo lo que se ha explicado durante este artículo. Sin embargo, es el momento de dejar la historia y pasar a la parte del teorema, que no es para nada complicado.
Aplicación del teorema
El teorema de ejes paralelos tiene como principal objetivo que se pueda rotar un objeto con respecto a varios ejes. En las tablas suele expresarse solo el momento de iniciar respecto al eje que puede atravesar el centroide. Una de las principales ventajas que da este teorema es la facilidad para poder calcular cuando se necesita hacer girar un cuerpo sobre ejes y estos no pueden coincidir.
Como el teorema de álgebra, este también se trata de explicar de una forma en la cual todas las personas que lean este artículo puedan comprender la forma en que se aplica. Un ejemplo claro en el cual se puede hacer uso de este teorema es: una puerta no gira por un eje que atraviesa su centroide, sino que es por un eje lateral donde se encuentran las bisagras. Es la forma sencilla en la cual se puede entender el teorema de ejes paralelos.
Se puede llegar a calcular la energía cinética que se aplica sobre el eje. Esto puede ser por que K es la energía cinética, I el momento de inercia sobre el eje y la w es la velocidad angular. Por lo que la formula que se aplica para este tipo de casos es la siguiente:
K = ½ I.ω2
A pesar de que la formula es similar a la que se utiliza para la energía cinética en un objeto de masa, esta es muy diferente. Debido a que también se considera la velocidad y es la siguiente: v: K =½ M.v2.
Enunciado del teorema de ejes paralelos
Considerando que un eje puede pasar por el centro de masa de un objeto sólido y puede presentarse un eje paralelo al primero, es en este caso donde se puede hacer una mención a que el momento de inercia de los dos ejes se puede expresar de la forma siguiente:
![]() donde se va a poder identificar los siguientes componentes de la formula, que es importante conocerlos:
donde se va a poder identificar los siguientes componentes de la formula, que es importante conocerlos:
- se trata del momento de inercia del cuerpo cuando se toma en cuenta el eje que no pasa por el centro de la masas.
- corresponde al momento de inercia del cuerpo cuando el eje si pasa a través del centro de masas del objeto.
- se refiere específicamente a la masa del objeto.
- corresponde a la distancia perpendicular que existe entre ambos ejes.
Se debe tener claro que el resultado que de la operación anterior puede llegar a usarse para poder tener el cálculo del tensor de inercia. Este puede darse de la forma siguiente, que también se necesita comprender:
donde:
- esta representa el vector con origen en O y el otro extremo en G.
- representa la matriz identidad.
Esto es lo básico que se debe aprender sobre el teorema de ejes paralelos. El cual hasta nuestros tiempos todavía sigue estando vigente. Estoy seguro de lo que estará por muchas décadas o siglos más.



 corresponde a la distancia perpendicular que existe entre ambos ejes.
corresponde a la distancia perpendicular que existe entre ambos ejes.
 esta representa el vector con origen en O y el otro extremo en G.
esta representa el vector con origen en O y el otro extremo en G. representa la matriz identidad.
representa la matriz identidad.