La trigonometría es una de las ramas de las matemáticas que se especializa en el estudio de las figuras geométricas. Partiendo desde este punto existen muchos puntos que deben ser estudiados y que se han creado durante los últimos siglos.
El teorema del coseno o también denominado como teorema de los cosenos, no hay tanta diferencia, se trata de uno de los resultados obtenidos en la trigonemetría y está se encarga de establecer una relación de proporcionalidad entre longitudes de lados de un triángulo con los cosenos de los ángulos que se ubican en el interior y son opuestos.
Se ha llegado a la conclusión de que el teorema del coseno se trata del resultado de generalizar el teorema de Pitágoras o por lo menos se puede decir que fue la base para poder llegar a este nuevo teorema. Sin embargo, es necesario profundizar un poco más para conocer a detalle lo que nos quiere decir este teorema.
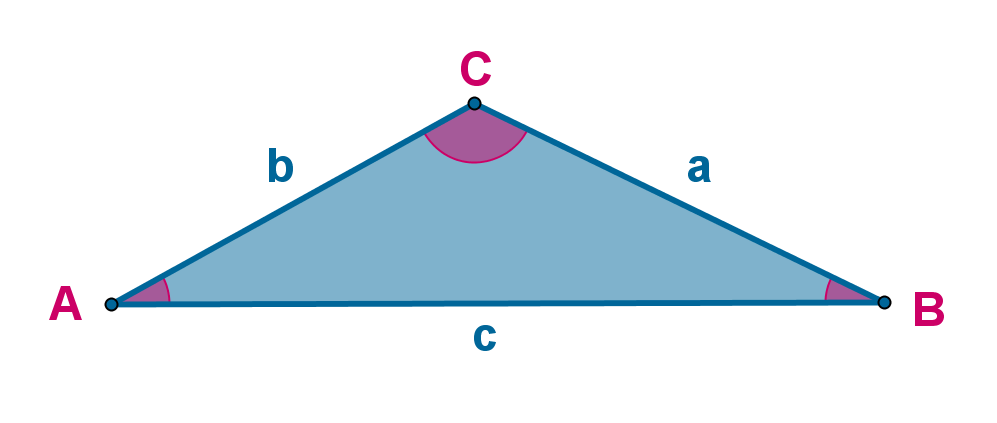
Nunca se debe considerar que un teorema es complicado de poder aplicar. En el caso del teorema del coseno es necesario tener claro que se necesita conocer la longitud de dos lados y la medida de un ángulo interior. El cual la regla marca que deberá ser opuesto al del otro lado.
Se necesita que se muestre el enunciado como también es ideal que se pueda demostrar el teorema, también será posible aprender a resolver los problemas de su aplicación. Esto cuando se quiere conocer la longitud o ángulo de un triángulo. Este teorema en algunos casos requiere de los resultados que pueden obtenerse mediante el teorema de Pitágoras, también se toma en cuenta que la suma de los ángulos interiores debe ser de 180°. Con esto se puede entender mucho del teorema del coseno.
Historia del teorema de coseno
Nos tenemos que remontar hasta el siglo III a.C. en la época de Euclides, mediante Los Elementos se puede encontrar que ya existía una idea sobre lo que sería la generalización del teorema de Pitágoras. En este caso se deberá de hablar respecto a las proposiciones 12 y 13 del libro II, en este se definen por separado casos de un triángulo obtusángulo y de triángulo acutángulo.
Una de las cosas más interesantes es que la formula que se empleo tiene la característica de que es arcaica. Esto se debe debido a que las funciones trigonométricas y algebraicas obligaron a los matemáticos de aquellas épocas a poder razonar solamente en las términos donde solamente se refería a las diferencias de áreas.
El propósito 12 establece lo siguiente:
En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso.
Euclides, Elementos.
Para entender un poco más sobre este teorema es necesario ver la siguiente imagen en la cual el triángulo ABC se muestra. El ángulo obtuso esta marcado con la letra C, mientras que BH es la altura respecto al vértice B. De tal forma que en épocas modernas este teorema se puede interpretar de la siguiente forma:
Sin embargo, no se ha quedado hasta ahí en la historia. Debido a que durante la Edad Media también tuvo aportaciones por parte de los matemáticos de las civilizaciones árabe y musulmanas. Durante esta época se pudo hacer que este teorema parte de la trigonometría pudiera expandir su forma y su alcance, en gran medida se debió al astrónomo y matemático llamado al-Battani.
Este científico tuvo la capacidad de poder generalizar el resultado que previamente ya había realizado Euclides. Este teorema ha sido fundamental para poder hacer el cálculo de la distancia angular entre el Sol y la Tierra. Ya llegando hasta el siglo XVII fue cuando se pudo llegar hasta el teorema en la forma que se conoce en la actualidad. Esto debido a que Euler pudo introducirlo en su libro Introductio in analysin infinitorum. Fue así como se pudo conocer el teorema del coseno.
Aplicación del teorema del coseno
Conocemos ya el teorema del álgebra o del valor medio. Un nombre por el cual también se le conoce se trata del teorema de Pitágoras generalizado. Se debe tener en cuenta que cuando el ángulo es recto o . Lo que sucede es que el teorema del coseno suele ser reducido a una formula, la cual se puede ver que es prácticamente el teorema de Pitágoras.
El teorema del coseno se podrá usar para triángulos que tengan un tercer lado y se conoce un ángulo y los lados que están adyacentes, la formula en este caso es fácil de aplicar:
Cuando se tiene los datos de los tres lados de un triángulo es posible usarlos para poder conocer solamente los ángulos. La formula que se utiliza para este caso tampoco es muy complicada de aplicar:
.
Ejemplos del teorema de los cosenos
Se debe considerar que se tiene un triángulo con lado un lado b que mide 45 centímetros y el lado c que mide 66 centímetros. El ángulo mide 47°, por lo que en este problema se requiere encontrar cuando mide el lado a del triángulo.

Como se requiere encontrar en específico cuando mide el lado a del triángulo se deberá aplicar la siguiente formula que pertenece al teorema del coseno:
![]()
En este caso los datos que se requieren son el lado b, el lado c y el ángulo α. Se deberá aplicar la formula de la siguiente manera:
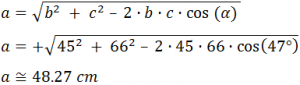
Finalmente, se tiene como resultado que el lado a tiene una longitud que es de 48.27 cm. Es así como se puede llegar a calcular y usar el teorema del coseno. No hay mucha duda, por lo que es claro y muy fácil de aplicarlo en cualquier situación que lo requiera.
Definitivamente, el teorema del coseno no están difícil de comprender en su forma moderna, para llegar a ella se requirió de muchas mentes. Es un trabajo de siglos.



 .
.

