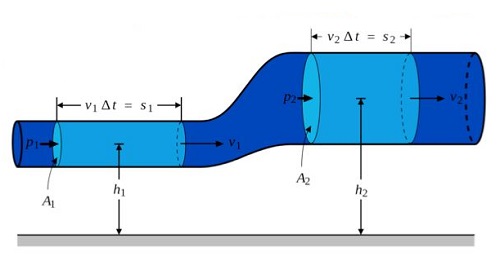
La física se ha considerado como una ciencia esencial para entender la complejidad del universo. Combinada con otros campos, permite una observación más minuciosa del objeto en estudio. Es así como la mecánica de fluidos, una rama de la física conjuntamente con la aplicación de conocimientos de mecánica básica, permite estudiar los fluidos tanto en reposo como en movimiento; en otras palabras, se enfoca en el movimiento de fluidos. A partir de esta, se desarrolla el teorema de Bernoulli, también conocido como el principio de Bernoulli; una postulación del científico suizo Daniel Bernoulli.
Este enunciado se enfoca en probar el comportamiento de un fluido que circula en una línea de corriente. Se establece que el fluido ideal no posee ningún tipo de viscosidad, y no está sometido a fricción. Así mismo, al encontrarse en circulación dentro de un conducto cerrado, si se cumplen estas características, su energía permanecerá constante.
La aplicación de este teorema se ha relacionado estrechamente con la ingeniería. Y puede ser usado para el estudio de distintos tipos de fluidos, por lo que se han detallado distintas formas de la ecuación de Bernoulli.
Tabla de contenidos
¿Qué es la mecánica de fluidos?
La mecánica de fluidos posee sus bases tanto en la física como en la mecánica. A través de esta se estudia el movimiento de los fluidos, las fuerzas que lo provocan y la interacción del fluido con el contorno del conducto por el que se mueve. A su vez, para la obtención de resultados, se basa en cuatro leyes: conservación de masa, conservación de cantidad de movimiento, primera y segunda ley de termodinámica.
Además, a esto se le suma la implementación de tres hipótesis para llevar a cabo los estudios de los fluidos:
- Hipótesis del medio continuo: esta hipótesis es solo aplicable dentro de la física clásica. Declara que el fluido permanece continuo dentro del espacio que lo contiene. Pero para llegar a esta conclusión, es necesario ignorar dos factores: la estructura molecular y la discontinuidad de la misma. Además, las propiedades de la materia pasan a ser consideradas como funciones constantes.
- Concepto de partícula fluida: para entender este enunciado, es necesario definir el término partícula fluida, que se conoce como una mínima porción de una masa fluida que cumple con dos características esenciales: ser lo suficientemente grande para contener un número diverso de moléculas y lo suficientemente pequeña para no verse afectada por la variación de las propiedades macroscópicas del fluido. Al cumplirse estas dos premisas, será posible asignarle un valor a cada una de las propiedades. El movimiento de esta partícula es igual a la velocidad macroscópica del fluido, por lo que en todo momento estará comprendida por las mismas moléculas.
- Descripción lagrangiana y euleriana del movimiento de un fluido: desde el punto de vista lagrangiano, se tiene que al hacer seguimiento de la partícula fluida, se pueden establecer funciones que permitan determinar su posición y características de manera continua. En el caso de la descripción euleriana, no tiene que ver directamente con la partícula fluida. A través de estas se establecen valores a las propiedades de los fluidos en puntos específicos del espacio, y en distintos instantes, dejando de lado el volumen diferencial que ocupa la partícula. Con este último enunciado, es que se pueden elaborar las ecuaciones generales de la mecánica de fluidos.

¿Qué es el teorema de Bernoulli?
El principio de Bernoulli se basa en el estudio del comportamiento de un fluido que se mueve a través de un sistema cerrado. El fluido en cuestión de cumplir con ciertas características para ser considerado como ideal; teniendo esto, se declara que durante su movimiento no debe existir rozamiento ni viscosidad. Y al encontrarse en un conducto cerrado, la energía permanece constante durante todo el recorrido.
Al tratarse de un postulado que tiene sus bases en la física y en la mecánica, se ha comprobado que puede derivarse de distintas leyes y teorías. En primer lugar, este teorema tiene influencias del principio de conservación de la energía, expresándose que al presentarse un flujo constante, la suma de todas las formas de energía de un fluido permanece constante en todos los puntos de la línea de flujo. De esta manera, dentro de este postulado se trabaja con las energías cinética, potencial e interna para obtener los resultados.
Pero también trabaja de la mano con la Segunda Ley del Movimiento de Newton, afirmando que al movilizarse un fluido en una línea horizontal desde una región de alta presión hacia una de baja presión, se concluye que existe mayor presión detrás del fluido, adquiriendo fuerza en el volumen, lo que permite darle aceleración a lo largo de la línea de corriente.
Ecuación del teorema de Bernoulli
Teniendo en cuenta la teoría, se tiene que el teorema trabajo únicamente con tres tipos de energía:
- Cinética: hace referencia a la velocidad que posee un fluido.
- Potencial: relacionada con la altitud que posee un fluido.
- De presión: equivale a la energía de un fluido resultado de la presión a la que está sometido.
A partir de estas, se establece la siguiente fórmula:
Definiendo las variables:
- V = velocidad del fluido
- p = densidad del fluido
- P = presión del fluido en la línea de corriente
- g = aceleración gravitatoria
- z = altura en la dirección de la gravedad
A través del enunciado de la fórmula, se establece que la suma de estas tres energísa es constante, por lo que si una varía, debe existir un cambio en alguna de las otras dos para mantener la constancia.
Historia del teorema de Bernoulli
Fue Daniel Bernoulli quien presentó al mundo este postulado. Pero para llegar a esta conclusión, tomo en cuenta las teorías que otros habían presentado con anterioridad. En 1598, Benedetto Castelli refuta las ideas propuestas por Giovanni Fontana en relación a su método para medir en ríos. Presenta una nueva perspectiva, donde incluye otros factores: la sección y la velocidad; además, aclara que cuando la medición se realiza en orificios, no solo se debe tomar en cuenta la variable del tamaño de estos, sino también la carga. A partir de este enunciado, desarrolla la Ecuación de Castelli: Q = AV.
Se presenta una nueva hipótesis en 1638, cuyo autor es Galileo Galilei. Afirmaba que un cuerpo presenta una aceleración uniforme durante una caída al vacío. Así presenta un teorema, basándose en las premisas de que existe una relación entre la velocidad uniforme de un cuerpo al caer al vacío con la velocidad uniformemente acelerada del mismo. Tomando este postulado y la Ecuación de Castelli, Evangelista Torricelli estableció el chorro que se produce al salir un líquido por un orifico de un tanque, tiene la forma de hipérbola de cuarto orden. Así mismo, declaró una similitud entre el chorro que sale de un tanque, con cuerpo cayendo al vacío desde la misma altura del tanque. Esto es complementado con la hipótesis de Isaac Newton, que agrega como una variable la presencia de un hielo en la superficie del tanque, lo que genera una presión para que el agua salga a través del orificio.

Es entonces 1738, que Daniel Bernoulli decide resolver el enigma, y presenta un experimento donde observa la salida de agua a través de un orificio de un tanque. Tras obtener los datos necesarios, afirma que el chorro no posee la misma velocidad que un cuerpo cayendo al vacío, pero que si tiene es capaz de adquirirla rápidamente. Sin embargo, esta deducción es mejorada por Johann Bernoulli, creando una ecuación más precisa, que es la que actualmente se maneja para el teorema de Bernoulli.
Aplicaciones del teorema de Bernoulli
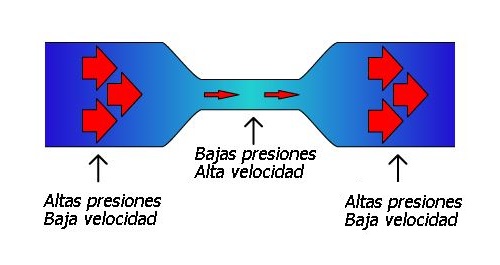
Las aplicaciones del teorema de Bernoulli pueden ir desde el campo profesional, como la ingeniería, hasta la vida cotidiana. Un ejemplo claro son las chimeneas de los hogares, cuya boca suele estar ubicada a una gran altura para aprovechar la velocidad del viento. Si este sopla muy rápido, entonces la presión será más baja, creando una diferencia entre las presiones de la boca y de la base, creando un entorno propicio para la combustión. En los deportes también puede ser aplicable, destacando la natación. Un nadador al realizar brazadas, corta el agua lo que genera una menor presión, pero que a su vez favorece la propulsión del cuerpo.
Pero existen casos más elaborados, como el carburador de un auto. La presión del aire fluye a través de este, y desciende en los puntos donde pasa por un estrangulamiento. En el momento en que esto ocurre, se inicia el flujo de gasolina, vaporizándose y mezclándose con la corriente del aire.
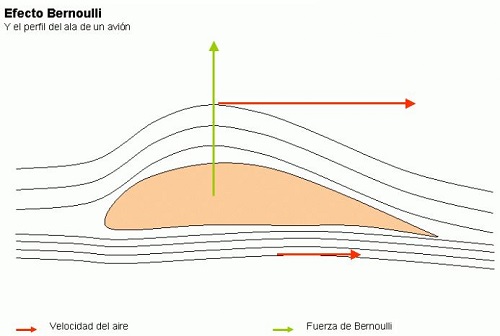
Una de las aplicaciones más resaltantes, se responde con la interrogante de por qué vuelan los aviones. Para lograrlo, es necesario aplicar el principio de Bernoulli en el diseño de las alas. La parte superior del ala de un avión se conoce como extradós, y la parte inferior intradós. La forma de la primera es mucho más curva que la de la segunda. Al aumentar la velocidad de la masa superior de aire, disminuye la presión, lo que permite que el avión permanezca suspendido en el aire y pueda volar sin problemas.