El cálculo vectorial se trata de un área de las matemáticas que se ha encargado de un análisis real de multivariables centrada en los vectores. Puede ser solamente en dos o más dimensiones. Se tiene en este caso la determinante de la geometría diferencial que es un conjunto de fórmulas y técnicas para dar solución a problemas que se presentan en la ingeniería y física.
Dentro del cálculo vectorial existe la posibilidad de hablar respecto al teorema de la divergencia. También se ha denominado como el teorema de Gauss o el teorema de Gauss-Ostrogradsky. De una forma sencilla se puede decir que este teorema se encarga de relacionar el flujo del campo vectorial sobre una superficie cerrada con la integral de su divergencia.
El volumen se encuentra delimitado la superficie. Es necesario tener en cuenta que se concibe la suma de todas las fuentes menos la suma de todos los sumideros da el flujo de salida neto de una región. Este tipo de resultados se puede dar como importante física, electrostática y dinámica de fluido. Toda está información se hace de manera general, pero es necesario abordar un poco más a fondo que hay mucho más por conocer.
Tabla de contenidos
¿Qué es la convergencia y la divergencia?
Se necesita tener muchos conceptos básicos para poder entender el tema del cual se esta hablando en este artículo. Nunca se debe ser una mente cerrada, debido a que esto bloquea el aprendizaje.
La convergencia se trata de dos o más cosas que tienen un punto de unión, esto se puede decir que se trata de una concentración. Mientras que la divergencia se trata de la separación. Tomando en cuenta estos dos datos se puede seguir adelante con el tema que se esta planteando.
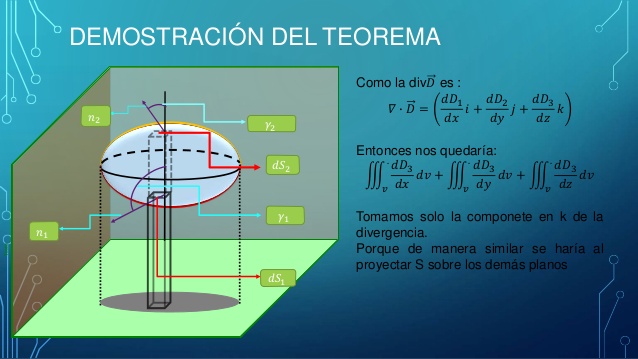
¿Qué es la divergencia espacial?
Se deberán entender muchas cosas antes de entrar más a fondo al tema. Uno de ellos es el concepto de divergencia, que para muchos no hay una definición clara. Yo lo tengo claro de que así es este tema tan necesario.
La divergencia de un campo vectorial se trata de una superficie cerrada que es reducida por completo al punto en el límite. Es necesario entender de que la divergencia de un campo vectorial también tiene una estrecha relación con el flujo que explica en el teorema de Gauss, que es el llamado teorema de la divergencia.
¿Qué es la divergencia de un campo vectorial?
Dentro de este mismo teorema es necesario comprender muchos aspectos que son información fundamental. Cuando hablamos del teorema de la divergencia se tiene que entender que es un campo vectorial.
Un campo vectorial se va a definir como la representación de un movimiento de un fluido. En tanto que la divergencia se trata de un operador que es capaz de tomar una función vectorial que logra definir al campo vectorial. Por lo tanto, este da como un valor de salida una función escalar que puede medir la densidad del fluido en cada uno de los puntos.
Historia del teorema de la divergencia
Joseph-Louis Lagrange conocido solamente como Lagrange, nació en la ciudad de Turín el 25 de enero de 1736 y falleció el 10 de abril de 1813. Fue un físico, matemático y astrónomo, el cual paso gran parte de su vida en Francia.
Se habla de este personaje debido a que en el año de 1762 fue quien estableció las bases para el teorema de la divergencia. Para después fuera Carl Friedrich Gauss quien diría continuidad en el año de 1813, luego fue George Green en 1825 y finalmente, fue Mikhail Vasilievich Ostrogradsky quien dio las variaciones de este teorema, el cual es conocido como teorema de Gauss, teorema de Green o teorema de Ostrogradsky.
Enunciado del teorema de la divergencia
Se deberá entender que y corresponden a dos subconjuntos de , donde se deberá tener claro que se trata de un simplemente conexo y el borde de , se usa para una curva regular o para poder regular trozos y cerrada.
Sea entonces que , un campo vectorial de clase , esto quiere decir que cuenta con derivadas parciales de primer orden continuas. Todo bastante claro hasta este punto. Yo tengo claro que para el teorema de la divergencia es necesario entender claramente cada uno de los detalles. Entonces:
Entonces:
se define como el vector el cual tiende a apuntar hacia el exterior del volumen. Dentro de esta formula se define como . Sin nada más que sea de sorprender esta parte fundamental del teorema de la divergencia.
Como tal este teorema se trata de una consecuencia del Teorema de Stokes, este se desprende también desde el Teorema fundamental del cálculo. En un principio este fue anunciado por el alemán Carl Friedrich Gauss en el año de 1835, el cual fue un matemático muy reconocido. Sin embargo, está fue publicada hasta el año de 1867.
El teorema de Gauss tiene una característica principal que indica que puede llegar a ser utilizado para la resolución de diferentes problemas de físicos. Mientras que estos se encuentren gobernados por las leyes inversamente proporcionales al cuadrado de la distancia.
Se puede hacer mención a la gravitación o intensidad de la radiación. Esta es llamada como la ley de Gauss, la cual también da para poder hablar sobre las ecuaciones de Maxwell. Sin embargo, se trata de otro tema que se debe también estudiar más a fondo. El teorema de la divergencia sigue siendo uno de los más importantes dentro de las matemáticas. Otros como el teorema de Norton también resulta importante.
¿Que es la Ley de Gauss?
A lo largo de este tema se ha mencionado a Gauss, es uno de los matemáticos principales dentro de este teorema de la divergencia. La Ley de Gauss que es la que está estrechamente relacionado con el teorema de la divergencia y el teorema de Gauss.
Se tiene el conocimiento de que la Ley de Gauss estabelce que el flujo un algunos campos a través de las superficies cerradas puede ser proporcional a un magnitud de las fuentes de la superficie, las cuales pueden ser de el interior.

 corresponden a dos subconjuntos de
corresponden a dos subconjuntos de  , donde
, donde  se deberá tener claro que se trata de un simplemente conexo y el borde de
se deberá tener claro que se trata de un simplemente conexo y el borde de  se usa para una curva regular o para poder regular trozos y cerrada.
se usa para una curva regular o para poder regular trozos y cerrada.




