La matemática es un campo que abarca muchas ciencias. A través de esta se han propuesto un sin número de postulados de gran utilidad tanto a nivel científico como cotidiano. De esta manera, encontramos la teoría de números, enfocada en el estudio de los números y sus propiedades, en su mayoría del conjunto de los enteros. Basándose en esta teoría, surge el teorema de Euler, un postulado que establece una proposición afirmando la divisibilidad de los números enteros.
Pero para lograr entenderlo, primero es necesario conocer un poco acerca del teorema de Fermat. Este plantea a primera instancia la proposición de divisibilidad de números, partiendo de la teoría de números. Y es que esta teoría, da pie a otro concepto utilizado por Leonhard Euler, un suizo especializado en matemática y física. Se trata del término congruencia, el cual afirma que el resto de dos números enteros a y b será igual al dividirlos por un número natural diferente de cero.

Sin embargo, se destaca el hecho de que Euler inició su investigación tomando en cuenta los aportes de Pierre de Fermat en su teorema. Es así, como se considera que el teorema de Euler es una generalización de este, llevando finalmente por nombre teorema Euler-Fermat.
Tabla de contenidos
¿Qué es la congruencia?
Entre los primeros conceptos a conocer para entender lo que se refiere el teorema de Euler, se encuentra la congruencia. Este término establece que dos números enteros, designados como a y b, tienen el mismo resto cuando son divididos por un número natural diferente a cero. Este número es conocido como módulo. Y este enunciado se representa de la siguiente manera:
a≡b (mod m)
Esta expresión puede entenderse como: a es congruente con b módulo m. Y puede ser representada de las siguientes formas:
- a mod m ≡ b mod m: el resto de a entre m es el resto de b entre m.
- m|a – b: divide exactamente a la diferencia de a menos b.
- ∃k∈Z a=b+km: a puede escribirse como la suma de b y un múltiplo de m.
Sin embargo, se reconocen dos sentidos en los que se puede aplicar el término congruencia. El primer caso va referido al teorema de Fermat, conocido como el pequeño teorema de Fermat. En este, se aplica el sentido de identidad matemática, en el cual se afirma que para cada número primo p y cada número entero a que no es divisible por p, se presenta la siguiente congruencia: ap-1≡1 (mod p).
Pero para el caso del sentido de ecuación. Este se presenta con una o más incógnitas, surgiendo la pregunta si una congruencia tiene solución. Cuando la respuesta es afirmativa, entonces se busca conocer cuáles son todas sus posibles soluciones.
¿Qué es el pequeño teorema de Fermat?
Una de las bases para el entendimiento del teorema de Euler, es conocer de qué se trata el pequeño teorema de Fermat. Este fue propuesto por el matemático francés Pierre de Fermat. Se considera que pertenece a los teoremas clásicos que conforman la teoría de números, encontrándose relacionado estrechamente con la divisibilidad.

El enunciado del teorema afirma que siendo p un número primo, se dice que para cada número natural a entonces: a>0, dándose la congruencia ap≡a (mod p). Aunque también ha sido definido de la siguiente manera: siendo p un número primo, se dice que para cada número natural a entonces: a>0, coprimo con p, entonces se tiene la congruencia ap-1≡1 (mod p). En otras palabras, cuando un número es elevado a la p-ésima potencia, y su resultado es dividido por a, se dice que el resto es divisible por p.
El pequeño teorema de Fermat ha tenido gran utilidad dentro de la criptografía asimétrica. Esta permite el encriptado de mensajes a través de dos claves criptográficas. La primera se enfoca en cifrar el mensaje, siendo pública, mientras que la segunda es para descifrarlo, siendo esta privada. La tecnología RSA se ha construido a través de las bases de este teorema.
¿Qué es el teorema de Euler?
En lo que respecta al teorema de Euler, se ha considerado como una generalización del teorema de Fermat. Finalmente, Euler afirma a través de este la divisibilidad de los números enteros. Es así, como se desglosa el siguiente postulado: Se tienen a y n, siendo estos números enteros primos relativos, entonces n puede dividir al número entero aφ(n)- 1. Sin embargo, también se presenta otro enunciado: Se tienen a y n que son números enteros primos relativos, entonces aφ(n) ≡ 1 (mod n).
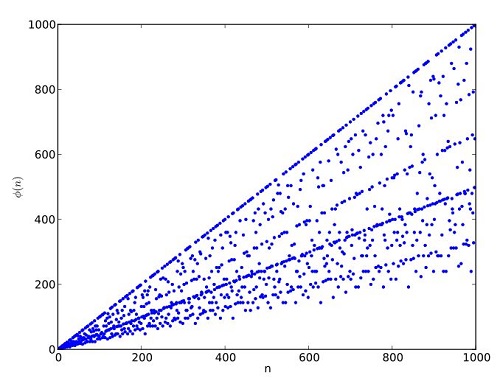
Dentro de ambas fórmulas destaca la función de Euler, representada por φ(n). Esta es definida como los números enteros positivos o iguales a n y coprimos con n. A través de esta, se puede determinar el tamaño del grupo multiplicativo de enteros modulo n.
Congruencias en el teorema de Euler
Dentro del teorema de Euler, se hace el uso del término congruencia, afirmándose que a y b son dos números congruentes con respecto a un módulo m, cuando m es dividido por un entero a-b. De esta manera, se presentan las siguientes congruencias, las cuales presentan un comportamiento similar a una igualdad:
- Se tiene que a≡b (mod m), entonces a+c≡b+c (mod m) y ac ≡ bc (mod m), siendo c cualquier número entero: se afirma que sumar o multiplicar una misma cantidad en ambos lados de la congruencia no afectará la relación.
- Se tiene que a≡b (mod m) y b≡c (mod m) entonces a≡c (mod m): se considera que es una relación transitiva.
El teorema de Euler y el pequeño teorema de Fermat
Ambos teoremas se encuentran estrechamente relacionados. Pierre de Fermat estableció su postulado, pero fue Leonhard Euler quien realizó la demostración del mismo. Se conoce que fue la primera prueba que afirmó la validez del teorema. Esta fue la base para lograr proponer su propia teoría, teniendo en cuenta lo que mencionaba Fermat.
Si bien el matemático francés estuvo al tanto de la prueba, omitió dar conocimiento de esta, afirmando simplemente la validez del teorema. Cuando Euler culmina su investigación, y presenta su postulado y realiza la respectiva demostración, es que se da a conocer el resultado de Fermat. Es así como este último se ha considerado como una consecuencia directa del teorema de Euler. Esto llevó a que se conociera popularmente como el teorema de Euler-Fermat.
