Las matemáticas se han convertido en una ciencia indispensable en la vida cotidiana de los seres humanos. De manera tal que, cualquier cosa que hagamos suele tener una explicación desde el punto de vista matemático. Para poder simplificar un poco la aplicación de esta ciencia, se han diseñado y desarrollado una serie de teoremas que facilitan el desarrollo y ejecución de determinados problemas matemáticos. Existe un teorema que, se puede considerar como la base fundamental de esta ciencia que, es conocido como el teorema de existencia.
Dentro de este caso se contemplan las ecuaciones. En principio fueron vistas únicamente como una forma sencilla de resolver problemas, pero no estaban incluidas dentro de las matemáticas. Posteriormente con el surgimiento de los distintos teoremas, se decidió incluirlas, estudiarlas y desarrollarlas de una forma más profunda.

Las ecuaciones han sido definidas como una igualdad matemática representada como dos expresiones, conocidas como miembros, que están separadas por un signo igual. Estas están compuestas por elementos conocidos e incógnitas, que se relacionan a través de operaciones matemáticas.
Tabla de contenidos
¿Qué es el teorema de existencia?
Una definición correcta para este tipo de teoremas, es la que señala que, se trata de un teorema que busca probar la existencia de una o más entidades, sin señalar cuantas son ni como hallarlas.
Existen múltiples ocasiones en las que por diversas circunstancias o situaciones fallamos al momento de obtener la solución definitiva de la ecuación diferencial dada, razón por la cual recurrimos a otros métodos para la solución de determinados problemas. La base primordial de la aplicación de este teorema consiste en satisfacer las cláusulas iniciales establecidas en la ecuación que se desea resolver.
La relevancia que ha ganado este teorema en las matemáticas, esto debido a que son pocos los teoremas en esta rama que involucran lo que conocemos como el cuantificador existencial. De manera general, se puede decir que el teorema de existencia es aquel utilizado para aseverar que, cada uno de los problemas que pertenecen a una determinada gama, la cual resulta bastante extensa poseen una solución que resulta muy particular.
Dicho en otras palabras, con este teorema no se busca el valor determinado de una variable, sino que se busca un criterio que permita determinar, si hay solución o no y si este puede ser utilizado para una diversidad de problemas. Generalmente este tipo de teoremas, se enuncia de la siguiente manera, “existe(n)…, o más generalmente ‘para todo x, y, …existe(n)”.
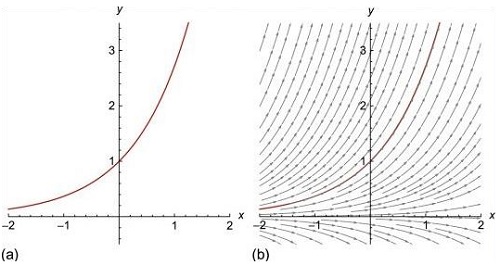
Desde el punto de vista matemático este teorema puede ser descrito de la siguiente manera, para una función dada f: X→ Y, la cual debe ser continua en el área limitada del plano x-y.
Uso del teorema de existencia
Hay que tener en cuenta que, en lo que se refiere a las matemáticas los teoremas de existencia y unicidad de solución, han alcanzado una gran importancia en lo que tiene que ver con el estudio de los problemas matemáticos y del cálculo. Generalmente, este teorema suele ser aplicado para la resolución principalmente de ecuaciones, muchas de las cuales resultan difíciles de responder, por lo que se hace necesario asegurarse de que exista una solución antes de intentar resolverlas.
Otra de las situaciones en las que se hace necesaria el uso de este teorema, es en el tipo de aplicaciones que representan lo que conocemos como un modelo matemático de tipo determinista sobre todo ante una situación física, para el cual exista solución. Además, este tipo de teorema es utilizado principalmente o en la mayoría de los casos para resolver casi todos los polinomios.
Así mismo, este teorema ha sido de gran utilidad para la resolución de ecuaciones diferenciales. Estas se conocen como un tipo de ecuación matemática caracterizada por relacionar una función con sus derivadas.
Condiciones o criterios para que se cumpla el teorema de existencia
Es importante destacar que, desde principios del siglo XX, existe una controversia que involucra principalmente a todos aquellos teoremas de existencia puros. Así mismo, se incluye la acusación que señala que al ser aceptados estos, se convierten en una traición a las responsabilidades de aplicación concreta de las matemáticas.
Es necesario hacer énfasis en que para la aplicación de este tipo de teoremas, los problemas deben caracterizarse por poseer una solución, que además esta debe ser única. Además este teorema solo es posible aplicarlo en el caso de las ecuaciones diferenciales de cualquier primer orden. Al tener una solución única, una vez que se repita el problema, ejercicio o experimento en las mismas condiciones, el resultado de este debe ser exactamente el mismo.
Importancia del teorema de existencia
Este es considerado como uno de los teoremas más importantes en lo que a teoría de las ecuaciones diferenciales ordinarias respecta. Y es que, cuando estamos en presencia de un determinado problema de valores iniciales, mejor conocido como problema de Cauchy, este teorema resulta ideal para la resolución de estos, debido a que cuenta con las siguientes condiciones: solubilidad y unicidad.
Cuando hablamos de un problema de Cauchy, nos referimos a un problema que está formado por dos elementos importantes, uno de ellos es la ecuación diferencial ordinaria y el otro una condición inicial. A través de este es posible resolver una ecuación de este tipo. Esto es posible teniendo en cuenta que una de las variables toma un valor en específico, lo que permite obtener las condiciones del sistema desde el inicio.
Cuando se habla del problema de Cauchy en ecuaciones diferenciales ordinarias, aquí se conocen previamente un conjunto de valores iniciales a través de los cuales se puede determinar con unicidad la estructura de la solución de la ecuación o sistemas de ecuaciones de cualquier orden. Si se trata de una ecuación diferencial lineal, se puede asegurar la existencia y unicidad de la solución siempre y cuando las funciones definidas en el problema se consideren diferenciables con continuidad.