El estudio de probabilidades a través de la estadística permite conocer la posibilidad de que un determinado evento pueda ocurrir, respondiendo todo tipo de interrogantes como la manera en que puede suceder o la frecuencia del mismo. Pero para lograr obtener los resultados de estos cálculos, es necesario seleccionar una población y una muestra, y un método que sea aplicable al caso de estudio. El teorema de límite central, conocido bajo las siglas TLC, permite realizar estudios probabilísticos con distribuciones de todo tipo.
Su enunciado declara que sin importar la distribución de las variables, que son generadas de manera aleatoria, la suma total de estas es gaussiana. La distribución de Gauss o distribución normal se conoce como una de las más aplicadas dentro de la estadística, trabajando con variables continuas, y cuya representación gráfica se asemeja a la de una campana.
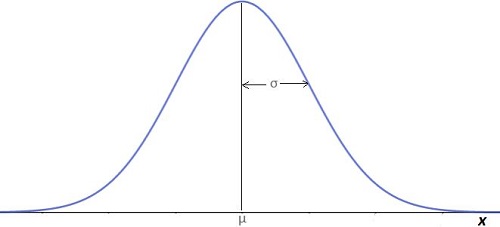
Además, existen otros dos términos que se manejan dentro de este teorema, y que también son básicos dentro de la teoría de probabilidades. En primer lugar aparece la media, también conocida como valor central, está definida como como el resultado de la suma de todas las muestras, dividido entre el número total de estas. También se encuentra la varianza, la cual es suma de las desviaciones elevadas al cuadrado, en relación a la media. El resultado es divido entre la cantidad total de muestras menos uno. Al entender estas definiciones, se tendrá la base para aplicar el teorema de límite central.
Es de importancia reconocer que dentro de la estadística y la teoría de probabilidad, el manejo de una distribución normal suele ser esencial. Este tipo de distribución es prácticamente aplicable en casi cualquier campo y cualquier caso de estudio. Por tal razón, es que la comprobación del TLC lo convierte en válido cuando el resultado tiende a una distribución normal.
Tabla de contenidos
¿Qué es el teorema de límite central?
El teorema de límite central declara que sin importar la distribución, la suma de todas las variables aleatorias generadas va a tender a una distribución normal o gaussiana. También se dice que las variables estudiadas no necesitan ser obligatoriamente normales, pudiendo trabajar con cualquier tipo, y obteniendo un resultado con esta misma distribución.
Otras de las declaraciones en torno a este teorema, afirma que es necesario que el tamaño de la muestra sea grande, utilizando un número grande de variables. Al realizar la suma de todas estas, se asegura que el teorema se cumple, si y solo si es igual a una distribución de Gauss. Si durante el estudio, se trabaja con la media, es válida la aplicación del teorema de límite central, ya que se realiza la suma de todos los datos, y se divide entre una constante.
En la definición de esta teoría, se habla de número de variables grandes. Esto se debe a que en su definición, se dice que n tiende a infinito. De esta manera, se establece la siguiente fórmula:
Zn=X-μσ/n
Donde n tiende a infinito.
Hay que terne en cuenta que el nombre de este teorema viene dado por la aproximación que existe entre dos distribuciones, siendo esta mayor en el centro, que en sus extremos. Así mismo, es aplicable dentro de distintos campos, destacándose dentro de la inferencia estadística y en la teoría de renovación.
Historia del teorema de límite central
El primer matemático que dio inicio al teorema de límite central fue Abraham de Moivre. Tras huir de Francia por la derogación del decreto de Nantes, termina en Londres, donde busca relacionarse con científicos de alto reconocimiento como Isaac Newton, dar a conocer sus conocimientos, más no logra nunca una cita académica que lo permita. Sin embargo, continuó con sus investigaciones dentro del campo de la estadística y el estudio probabilístico, enfocándose en el estudio de los límites en la distribución binominal. Durante los experimentos detalló que el número de ensayos aumenta sin límites, dando a lugar a un aumento dentro del exponencial de la función –X2/2. Estableció así la fórmula: 2/(B√n)(1/2n), en caso de que n posea valores grandes, donde Log(B)= 1-1/12+1/360-1/1260+1/1680.
James Stirling declaró que en el caso de B, este era igual a √2π, y estableció una fórmula para el cálculo de la distribución binominal, afirmando a su vez que la probabilidad del m=n/2 éxitos en ensayos de n=2m es igual a ((m!)(m!)/(2m)!)(1/22m), comprobando con esto la teoría de Moivre a través del factorial.
Pero quien dio inicio al postulado de la distribución normal, siendo el tipo de distribución que se obtiene tras la suma de distintas variables dentro del teorema de límite central, fue Thomas Simpson, quien encontró ciertos inconvenientes dentro de la distribución aplicada en la observación astronómica. Pero Carl Gauss profundizó en estas investigaciones, aunque a su vez, Pierre Simon de Laplace y Adrien-Marie Legendre, matemáticos franceses, se encontraban trabajando en sus propias ideas en torno a la distribución normal. Debida a que muchos expertos se encontraban realizando aportes en el tema, adquirió diferentes nombres. Según Gauss, siempre afirmó que él fue el primero en utilizar este procedimiento estadístico, asegurando que en el año 1794 fue que aplicó esta distribución por primera vez.
Sn embargo, Laplace añadió a su investigación las primeras ideas acerca del teorema. Su postulado fue tomado por el ruso P.L. Chebyshev, quien en compañía de sus estudiantes, empezó a realizar ensayos para comprobar su validez y desarrollar completamente para su correcta aplicación.
Propiedades del teorema de límite central
Para que la aplicación del teorema de límite central sea correcta, se debe cumplir una serie de condiciones o propiedades que aseguran su validez:
- Al trabajar con muestras de tamaño grande, esto asegura que la suma de las medias muestrales sea igual a una distribución normal. Según el teorema de límite central, se considera que una muestra es grande cuando supera un número mayor a 30. Con esto, se afirma que al tener una muestra superior a 30, la distribución de la media muestral tendrá tendencia a una distribución gaussiana. Este enunciado es válido para cualquier tipo de distribución con la que se trabaje.
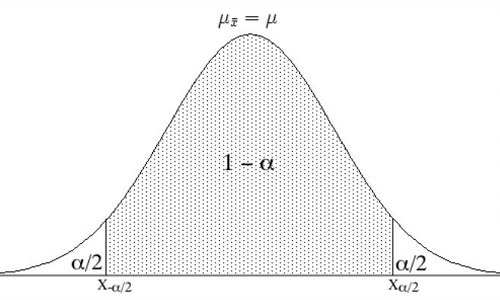
- La media muestral y la media poblacional siempre serán iguales, definiéndose de la siguiente manera: la media de la distribución de la media muestral será igual a la media de la población total estudiada.
- La varianza de la distribución de la media muéstrale está definida bajo la siguiente fórmula: σ²/n, donde σ² es la varianza de la población, y n es el tamaño de la muestra estudiada.
- Existen distintas manera de aplicar el teorema de límite central, y esto es posible dependiendo de los factores que aseguran la convergencia. De esta manera, se declara que las variables inmersas en el estudio, deben cumplir con ciertas condiciones: deben ser independientes, estar distribuidas de manera similar, contar con una media y varianza finita.
Tipos de muestras dentro del teorema de límite central
Se sabe que dentro del teorema de límite central se puede trabajar con distintas distribuciones, tendiendo el resultado final a una distribución normal. Así mismo, puede aplicarse en distintas muestras, destacándose:
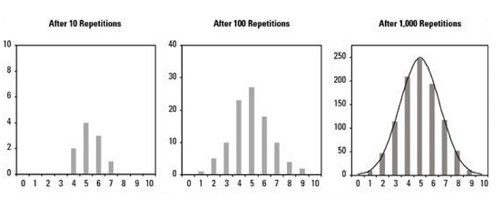
- Muestra de una población uniforme: una de las características propias de este tipo de muestra, es que posee una distribución uniforme, convirtiéndola en una población simétrica. Según el teorema de límite central, se considera aproximadamente normal a la distribución de las medias comprendida por 1000 muestras de tamaño 5.
- Muestra de una población exponencial: las características que identifican a una población exponencial es que son asimétricas y no normal. Pero en este caso, el teorema de límite central asegura que es aproximadamente normal la distribución de las medias comprendida por una muestra de 1000 de tamaño 50.
Ejemplo teórico del teorema de límite central
A través de un ejemplo, se puede demostrar el proceso de aplicación del teorema de límite central. Tomemos como caso de estudio a S&P 500, la cual es una compañía que posee más de 500 sucursales. Se busca analizar las rentabilidades medias, pero se tiene en cuenta que no es posible realizar un estudio de cada una al poseer poca información. De esta manera se toma la media poblacional.
Al decidirse a aplicar el teorema de límite central, se puede escoger una muestra para el análisis que comprenda un total de 500 sucursales de S&P 500. Como se sabe, para que sea válida su aplicación, es necesario que se cuente con una muestra mayor a 30, por lo que se cumple una de las condiciones. Finalmente, se determina un total de 50 empresas para iniciar, seleccionadas de manera aleatoria, y en cada una se aplica el mismo proceso de estudio. Según el enunciado del teorema, los pasos serías:
- Se establece una muestra de 50 empresas de S&P 500, y se obtiene la rentabilidad media del total de la muestra.
- Se vuelven a seleccionar continuamente otras 50 sucursales, y se realiza el mismo procedimiento.
- Al realizar la suma de todas las rentabilidades medias del total de las muestras que se escogieron para el análisis, esta debe ser aproximada a una distribución normal.
- Finalmente, las rentabilidades medias del total de muestras escogidas se aproximará a la rentabilidad media de la población total.
