El cálculo es una rama de la matemática que permite alcanzar resultados a través de la resolución de operaciones, mediante procedimientos específicos y relacionados con los datos que se desea hallar. El teorema fundamental de cálculo es uno de los enunciados matemáticos de mayor aplicación en distintas áreas. Pero para poder entenderlo en su totalidad, es necesario conocer terminología básica que facilita su aplicación.
El primer término que se debe identificar es la función, siendo una de las bases dentro del cálculo. Está definida como una relación entre dos conjuntos, donde los elementos contenidos en el primer conjunto les corresponden únicamente un elemento del segundo conjunto, o en tal caso, ninguno. Sobre las funciones se pueden aplicar operaciones, que permita dar solución a una incógnita.
Uno de estos casos, son las derivadas, que se consideran como uno de los conceptos de mayor relevancia dentro de las matemáticas. Se encuentran definidas como el resultado del límite de una función, representando la variación de esta a partir de que en su entrada se registran cambios. A su vez, también se puede aplicar sobre una función la integración, un procedimiento definido como la inversa de la derivación, pudiendo obtener a través de esta la función primitiva de una función.
Son estos dos último términos los que permiten la formulación del teorema fundamental de cálculo, declarando que se tratan de operaciones inversas. De esta manera, se afirma que la derivada de la integral de una función es ella misma. Sin embargo, en algún momento de la historia, se ignoraba que ambos términos estuvieran vinculados.
Tabla de contenidos
¿Qué es una función?
Uno de las definiciones básicas que se debe manejar dentro de cualquier teoría de cálculo, es el término función, siendo definido como una relación entre dos conjuntos: el primero conocido dominio, y el segundo rango. A los elementos del primero, denominados variable independiente, les corresponde un único elemento del segundo, denominados como variable dependiente. Puede existir el caso de que no se asigne ningún elemento. Se deduce así que los elementos del rango son dependientes de los elementos del dominio.
Las funciones se ubican dentro de la rama de análisis matemático, y para representarlas, se utiliza una letra minúscula, seguida de otra letra minúscula entre paréntesis, que hace referencia al elemento del dominio al cual se desea encontrar una imagen en el conjunto de rango. Aunque en términos generales se declara que solo se asigna un único elemento, existen funciones que permiten que una variable dependiente corresponda a más de una variable independiente en el primer conjunto.

¿Qué es una derivada?
Dentro de las matemáticas, las derivaciones son solo aplicables a funciones. Se definen como un método para calcular una función, tomando en cuenta que los valores iniciales de esta varían. También se puede afirmar que se trata del resultado del límite de una función dada, pudiendo ser representada como la pendiente de la recta tangente a la curva de la función en un punto.
Gráficamente se tiene que una derivada es una recta superpuesta sobre una curva, que representa la función. Para que se cumpla el enunciado de derivada, la línea debe encontrase en los puntos extremos de la curva, haciendo referencia al límite de una función comparándolo con el incremento que sufre la variable la variación del valor de esta.
¿Qué es una integral?
Cuando se habla de integración, se hace referencia a una operación inversa a la derivada. Es así como se define que una integral es la función de otra función conocida como primitiva. Dicho en otras palabras, el procedimiento permite que la función regrese a su estado original, partiendo desde una derivada. También es conocida bajo el nombre de antiderivada.
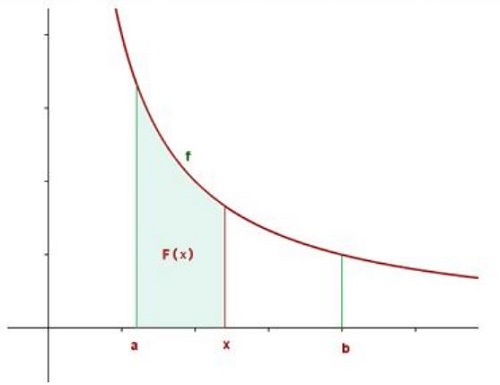
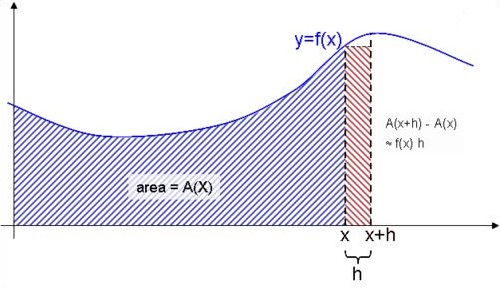
De manera gráfica, la integral puede ser representada como el área dibujada bajo la curva de una función dada. Puede ser positiva o negativa según los valores que se manejen en la función. Ha sido de gran aplicación en investigaciones científicas y la ingeniería.
¿Qué es el teorema fundamental del cálculo?
ES mediante el teorema fundamental del cálculo que se comprueba que las operaciones de integración y derivación guardan estrecha relación, siendo considerada una la inversa de la otra. Según el enunciado establecido, se afirma que toda función es integrable si se logra comprobar que la derivada de su integral es su primitiva. Esta teoría puede ser aplicada tanto en funciones continuas como discontinuas.
Es necesario aclarar que dentro de este teorema, se utilizan las integrales definidas, siendo un procedimiento necesario para el cálculo del valor del área limitada por la curva y la recta de una función. El teorema fundamental de cálculo cuenta con dos postulados para poder comprobar que ambas operaciones son la inversa de la otra.

Primer teorema fundamental del cálculo
A través del primer enunciado, se establece que toda función continua dentro de un intervalo definido posee primitivas. En términos matemáticos queda definido:
- Una función f integrable dentro de un intervalo [a,b], se define F sobre [a,b] por Fx=axf(t)dt, estableciendo que f es continua en c∈(a,b), determinando que F es derivable en c y F’c=f(c).
De esta manera, se afirma que siempre que la función sea continua en un intervalo, esta tendrá una primitiva.
Segundo teorema fundamental del cálculo
El segundo enunciado se establece muy similar al primero, pero destacando la propiedad de que no necesariamente la función tiene que ser continua.
- Sea f una función integrable dentro del intervalo [a,b], y F'(x) una función primitiva de f, entonces: abfxdx=Fb-F(a).
Esta segunda parte del teorema fundamental del cálculo también es conocida bajo el nombre de Regla de Barrow.
Historia del teorema fundamental del cálculo
Actualmente, se ha reconocido que el teorema fundamental del cálculo hace referencia a la relación existente entre la derivación y la integración, siendo estas operaciones inversas. Pero es de destacar que en la antigüedad, esta propiedad se desconocía, y para los conocedores, eran dos procedimientos distintos y aislados.
Para el momento, en Grecia los matemáticos utilizaban un método diferente para el cálculo del área. Estos matemáticos utilizaban infinitesimales para llevar a cabo estas operaciones, para más adelante transformarlo en lo que hoy conocemos como la integración. Lo mismo sucedió con la derivación Durante el siglo XIV, las investigaciones en torno a la continuidad de funciones y el movimiento quedó en manos de un sector reducido, destacándose los calculadores de Oxford. Esto impidió que se observara fácilmente la relación entre los procedimientos.

James Gregory fue el primer matemático que destacó que las integrales y las derivadas eran operaciones inversas, aunque lo explicó de manera básica y superficial. Este trabajo expandido por Isaac Barrow, dando postulados más específicos y desarrollando la Regla de Barrow utilizada en el segundo teorema fundamental del cálculo. La teoría llamó la atención de Isaac Newton, quien decidió dar su aporte y complementarlo. Pero no fue sino gracias a Gottfried Leibniz que se estableció de manera concreta el teorema que conocemos en la actualidad, introduciendo además el cálculo de cantidades infinitesimales.