El nombre de Herón es bien conocido en el campo de las matemáticas por sus aportes en forma de métodos y fórmulas. Herón de Alejandría fue un matemático e ingeniero del siglo I y II después de Cristo. También es conocido por inventar la primera máquina de vapor.
Compuso una obra literaria llamada “Métrica”, donde aporta métodos matemáticos bien complejos acerca del campo de la geometría. En dicha colección (cuenta con 3 libros), se registra una fórmula, también conocida como el Teorema de Herón.
Tabla de contenidos
En qué consiste el Teorema de Herón
Comúnmente en geometría, a la hora de calcular el área de un triángulo es necesario saber la amplitud de la base y de la altura. La fórmula más conocida para ellos es que el área de un triángulo es el semiproducto de las dos longitudes anteriores. Pero según Herón, esto no es necesario.
Otra forma de calcular el área según Herón
El Teorema de Herón te da otra perspectiva ante la problemática de no tener la longitud de la altura. En su defecto debes conocer las dimensiones de los 3 lados del triángulo. Esto te permite calcular el área sin conocer la altura. Pero antes de hacerlo, debes saber qué es el semiperímetro.
El semiperímetro
El término es usado a la hora de formular el Teorema de Herón, por lo que es importante estar claro de qué significa. Como semi perímetro se define la semisuma de los tres lados del triángulo. Una vez claro de esto, ya puedes calcular el área de un triángulo sin necesariamente tener la altura del mismo.
El área a partir del semiperímetro
Partiendo del conocimiento del semiperímetro, el área es sencilla de calcular por el Teorema de Herón. Va a ser igual a la raíz cuadrada del semiperímetro multiplicado por la diferencia del semiperímetro por cada uno de los lados. Esto se define de la siguiente forma:
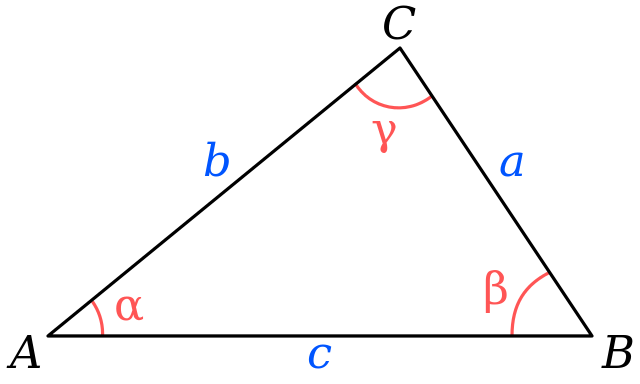
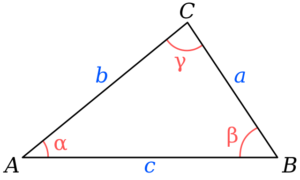
A=s(s-a)(s-b)(s-c)
Donde A es el área del triángulo, s es el semiperímetro y a,b,c son los lados del triángulo.
Esta deducción es fácilmente demostrable por trigonometría. Partiendo de la idea que el área también puede ser hallada por el semiproducto de las longitudes de dos lados adyacentes por el seno del ángulo comprendido entre ambos, es fácil llegar a la suposición de esta fórmula.
Esta prueba anterior se le conoce como la prueba por la Ley se los cosenos. Además, también es demostrada a partir del Teorema de Pitágoras.
Es totalmente infalible el Teorema de Herón
Se comprobó que el Teorema de Herón es numéricamente inestable. Se amplió el uso de esta fórmula, no solo al uso de las geometrías sino también a la astronomía. En este campo se comprobó dicho fallo. Para ángulos muy pequeños el Teorema de Herón presentaba la citada inestabilidad numérica. Para ello fue necesario hacer una reorganización de los términos de la fórmula.
Adaptación de la fórmula de Herón
La solución fue hacer un ajuste a la hora de tomar las longitudes de los lados. En este caso en lugar de tomar aleatoriamente los lados, se toma el lado a como el mayor, b como el lado de longitud media y c como el más pequeño. Quedando de la siguiente forma la fórmula:
A=14(a+(b+c))(c-(a-b))(c+(a-b))(a+(b-c))
Mediante esta sucesión de paréntesis se evita la inestabilidad presente en la anterior versión del Teorema de Herón.
Triángulo de Herón
A partir del teorema anterior se denomina a cierto tipo de triángulo como de Herón.
Cuál es el Triángulo de Herón
Es aquel que todos sus lados tienen longitudes enteras, así como su área. De esta forma es fácilmente deducible que cualquier triángulo rectángulo de lados enteros es un triángulo de Herón.
Otro ejemplo es si pegas dos triángulos rectángulos de lados 3,4,5 justo por la parte donde está el cateto que mide 4 unidades. Así, tendrías un triángulo isósceles de longitudes 5,5,6 y 12 unidades cuadradas de área.
Teorema de Herón y los polígonos
El Teorema de Herón no es solo aplicable a la resolución de áreas de triángulos, sino que se presta para más aplicaciones. Puede que necesites calcular el área de determinado polígono y esta fórmula puede ser tu solución. Si el polígono en cuestión cuenta con varios lados, no puedes aplicar otra fórmula conocida.
En cualquier figura de varios lados es posible formar triángulos internos, de modo que puedas calcular el área de los mismos. Por consiguiente, la suma de las áreas de todos los triángulos, sería igual al área del polígono en sí.
El único problema que se presentaría ante tal situación es determinar la longitud de las diagonales que se forman al trazar dichos triángulos. Pero por métodos trigonométricos la solución es muy evidente. De cualquier forma, es una vía más eficaz y rápida para determinar el área de un polígono no conocido.
Teorema de Herón para calcular un volumen
La fórmula también es usada en el campo del álgebra. Si deseas calcular el volumen de determinada dimensión, el Teorema de Herón también tiene la respuesta.
Si defines n como un conjunto de vectores linealmente independientes agrupados por filas en una matriz A, entonces es posible calcular el volumen de dimensión n. En teoría este es el resultado del volumen de una figura de n dimensiones.
Volumen(A)=1n!det(A∙At)
En este caso, At es la matriz traspuesta de A, det es el determinante y n! es el factorial del total de dimensiones. Esta generalización permite calcular el volumen de determinado polígono a partir de sus aristas.
La fórmula de Herón y la fórmula de Brahmagupta
Pudiera decirse que la fórmula de Herón es un caso particular de la fórmula de Brahmagupta. Esta última se emplea para el cálculo del área de cuadriláteros inscritos en una circunferencia. Pero a la vez, ambas son casos particulares de la fórmula de Bretschneider para el cálculo del área de un cuadrilátero.
De igual forma parten del hecho de conocer las longitudes de los lados del triángulo y calcular el área del mismo. Siempre deben cumplirse los requerimientos de la desigualdad triangular. De no cumplirse, los resultados darían erróneos o falseados.
Desigualdad triangular
La desigualdad triangular se basa en el cumplimiento de los siguientes puntos:
a+b>c
b+c>a
c+a>b